TBH个人博客
算法总结——数组
tbghg
  2022-07-09 16:10:51   2022-07-09 16:10:51    11.5k 字  51 分钟

数组

[TOC]

1. 前缀和

我们先从问题出发引出前缀和，现在给定一个数组q[8] = {1, 2, 5, 3, 7, 9, 4, 5 }要求计算给定区间的和，如 [ 1 , 2 ] --> 2 + 5 = 7 , [ 3 , 6 ] --> 3 + 7 + 9 + 4 = 23。
这个题目我们直接遍历即可，但是如果要算的区间较多呢，例如给出300次询问，那我们便要进行300次遍历。数组长度为n，询问次数为m，则时间复杂度为o(nm)。

接着我们引出前缀和，所谓前缀和，就是从位置0到位置i这个区间内的所有的数字之和。对于例子中给出的数组我们用sum[8]来表示前缀和，即sum[i] = q[0] + …… + q[i]，我们可以推出：sum[0] = q[0] , 当 i > 0时sum[i] = sum[i-1] + q[i]。所以我们通过一次遍历便可求出数组的前缀和。

1
2
3
4
5
6
7
8
9
int main() {
    int q[8] = {1, 2, 5, 3, 7, 9, 4, 5};
    int sum[8];
    sum[0] = q[0];
    for (int i = 1; i < 8; i++) {
        sum[i] = sum[i - 1] + q[i];
    }
    return 0;
}
1
2
3
4
5
6
7
8
9
func main() {  
	a := []int{1, 2, 3, 4, 5, 6, 7, 8}  
	sum := make([]int, len(a))  
	sum[0] = a[0]  
	for i := 1; i < len(a); i++ {  
		sum[i] += sum[i-1] + a[i]  
	}  
	fmt.Println(sum)  
}

经过观察可以发现，如果我们要求区间[4, 7]（数组下表）的和，我们只需要将前8位的和减去前4位的和，属于o(1)量级的计算。可以得出计算区间[L, R]的和的公式为sum[R] - sum[L-1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int main() {
    int q[8] = {1, 2, 5, 3, 7, 9, 4, 5};
    int sum[8];
    sum[0] = q[0];
    for (int i = 1; i < 8; i++) {
        sum[i] = sum[i - 1] + q[i];
    }
    int m, L, R; // m代表询问次数
    scanf("%d", &m);
    for (int i = 0; i < m; i++) {
        scanf("%d %d", &L, &R);
        printf("%d\n", sum[R] - sum[L - 1]);
    }
    return 0;
}

接着我们将前缀和拓展到二维

同样的，我们现在有一个二维数组如下：

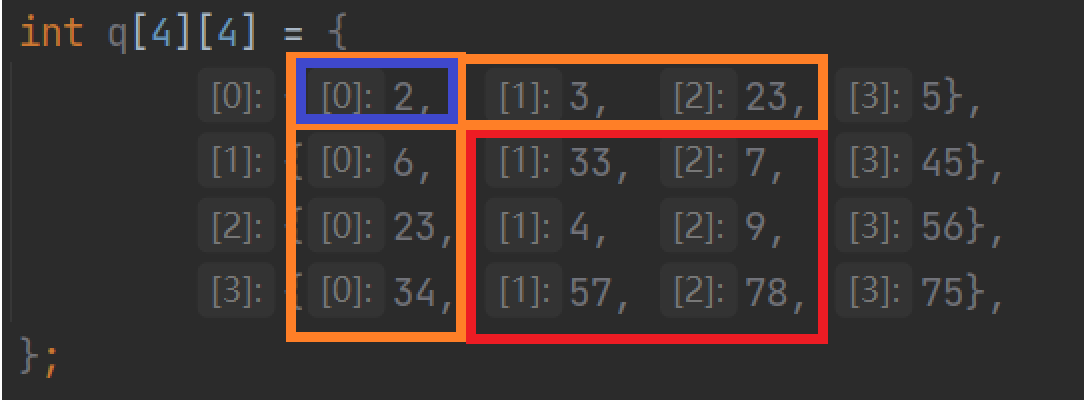
1
2
3
4
5
6
int q[4][4] = {
    {2,  3,  23, 5},
    {6,  33, 7,  45},
    {23, 4,  9,  56},
    {34, 57, 78, 75},
};

现在需要给出区域范围求出相应的区域和，例如给出[1, 1]~[3, 2] --> q[1][1] + q[1][2] + q[2][1] + q[2][2] + q[3][1] + q[3][2] = 188

接着采用前缀和的思想我们将sum[i][j] 记为[0, 0]~[i, j]的区域和。

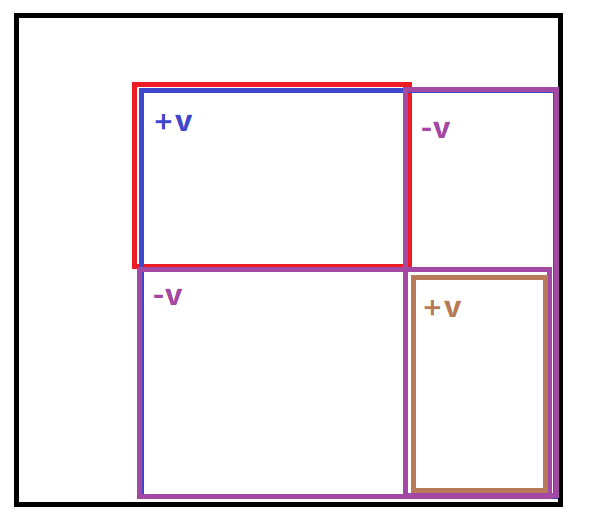
如果我们要求[x1, y1]~[x2, y2]的区域和时，通过下表（图以[1, 1]~[3, 2]进行举例）可以直观看出，最终结果为整个大框减去两个橙色框加上重复减去的蓝色框，即：ans = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]

image

这时我们可以推出sum[i][j] = sum[i - 1][j] - sum[i][j - 1] + sum[i - 1][j - 1] + q[i][j]，借此迭代出sum。

考虑到数组越界，我们需要将i和j为0的情况单独计算

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int q[4][4] = {
    {2,  3,  23, 5},
    {6,  33, 7,  45},
    {23, 4,  9,  56},
    {34, 57, 78, 75},
};
int sum[4][4];

int main() {
    sum[0][0] = q[0][0];
    for(int i = 1;i<4;i++) sum[i][0] = sum[i-1][0] + q[i][0];
    for(int j = 1;j<4;j++) sum[0][j] = sum[0][j-1] + q[0][j];
    for(int i = 1;i<4;i++)
        for(int j = 1;j<4;j++)
            sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + q[i][j];
    return 0;
}

最后我们分为 x1 = y1 = 0、x1 = 0, y1 != 0、y1 = 0, x1 != 0及其他 四种情况计算ans

  1. x1 = y1 = 0时，ans = sum[x2][y2]
  2. x1 = 0, y1 != 0时，相当于不需要考虑上侧的橙色框，只需减去左侧的橙色框ans = sum[x2][y2] - sum[x2][y1 - 1]
  3. y1 = 0, x1 != 0时，相当于不需要考虑左侧的橙色框，只需减去上侧的橙色框ans = sum[x2][y2] - sum[x1 - 1][y2]
  4. 其他，ans = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1]
1
2
3
4
5
6
int calcResult(int x1, int y1, int x2, int y2) {
    if (!x1 && !y1) return sum[x2][y2];
    if (!x1) return sum[x2][y2] - sum[x2][y1 - 1];
    if (!y1) return sum[x2][y2] - sum[x1 - 1][y2];
    return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
}

完整代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<stdio.h>

int q[4][4] = {
        {2,  3,  23, 5},
        {6,  33, 7,  45},
        {23, 4,  9,  56},
        {34, 57, 78, 75},
};
int sum[4][4];

int calcResult(int x1, int y1, int x2, int y2) {
    if (!x1 && !y1) return sum[x2][y2];
    if (!x1) return sum[x2][y2] - sum[x2][y1 - 1];
    if (!y1) return sum[x2][y2] - sum[x1 - 1][y2];
    return sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
}

int main() {
    sum[0][0] = q[0][0];
    for (int i = 1; i < 4; i++) sum[i][0] = sum[i - 1][0] + q[i][0];
    for (int j = 1; j < 4; j++) sum[0][j] = sum[0][j - 1] + q[0][j];
    for (int i = 1; i < 4; i++)
        for (int j = 1; j < 4; j++)
            sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + q[i][j];
    int m,x1,x2,y1,y2;// m代表询问次数
    scanf("%d",&m);
    for(int i=0;i<m;i++){
        scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
        printf("%d", calcResult(x1, y1, x2, y2));
    }
    return 0;
}

例题1 长度最小的子数组

题目

题目链接

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的连续子数组并返回其长度。如果不存在符合条件的子数组，返回 0 。

要求时间复杂度不超过O(nlogn)

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：
输入：target = 4, nums = [1,4,4]
输出：1

示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

其中：

  • 1 <= target <= 10^9
  • 1 <= nums.length <= 10^5
  • 1 <= nums[i] <= 10^5

分析

本题可以采用前缀和 + 二分查找的方式求解，在大一C语言课程中我们应该已经学到过二分查找，这里对二分查找仍不熟悉的同学请将 [附加题](#附加题 二分查找) 认真完成，当然我们在查找与排序模块会对二分查找进一步学习。

如果我们采用暴力解法（两层for循环直接跑）时间复杂度为o(n^2)显然不太合适，这里因为需要对区域进行求和我们可以考虑前缀和，因为所有数均为正整数，前缀和为有序数组，我们可以用二分查找快速定位到目标位置。

整体过程为创建一个数组 sums 用于存储数组 nums 的前缀和，其中 sums[i] 表示从 nums[0] 到 nums[i−1] 的元素和。得到前缀和之后，对于每个开始下标 i，可通过二分查找得到大于或等于 i 的最小下标 bound，使得 sums[bound]−sums[i−1]≥s，并更新子数组的最小长度（此时子数组的长度是 bound−(i−1)）。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
int lower_bound(int *sums, int l, int r, int target) {
    if (sums[r] < target) return -1;
    while (l < r) {
        int mid = l + (r - l) / 2;	// 等同于(l+r)/2，防止越界
        if (sums[mid] >= target) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    return l;
}

int minSubArrayLen(int s, int *nums, int numsSize) {
    if (numsSize == 0) {
        return 0;
    }
    int ans = INT_MAX;
    int *sums = (int *)malloc(sizeof(int) * (numsSize + 1));
    // 为了方便计算，令 size = n + 1
    // sums[0] = 0 意味着前 0 个元素的前缀和为 0
    // sums[1] = A[0] 前 1 个元素的前缀和为 A[0]
    // 以此类推
    for (int i = 1; i <= numsSize; i++) {
        sums[i] = sums[i - 1] + nums[i - 1];
    }
    for (int i = 1; i <= numsSize; i++) {
        int target = s + sums[i - 1];
        int bound = lower_bound(sums, 1, numsSize, target);
        if (bound != -1) {
            ans = ans < bound - (i - 1) ? ans : bound - (i - 1);
        }
    }
    return ans == INT_MAX ? 0 : ans;
}

课后作业

题目链接

对一个给定的自然数M，求出所有的连续的自然数段，这些连续的自然数段中的全部数之和为M。

例子：1998+1999+2000+2001+2002 = 10000，所以从1998到2002的一个自然数段为M=10000的一个解。

输入格式
包含一个整数的单独一行给出M的值（10 < M < 2,000,000）。

输出格式
每行两个自然数，给出一个满足条件的连续自然数段中的第一个数和最后一个数，两数之间用一个空格隔开，所有输出行的第一个按从小到大的升序排列，对于给定的输入数据，保证至少有一个解。

1
2
3
4
5
6
7
8
// 样例输入
10000

// 样例输出
18 142 
297 328 
388 412 
1998 2002

作业答案

这道题目有多种解法，在此我们可以考虑通过前缀和的方式求出区间和，通过二分查找缩短时间复杂度，与例题类似，在此不过多解释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include "stdio.h"
#include "malloc.h"

int lower_bound(long long *sum, long l, long r, long long target) {
    while (l < r) {
        long middle = l + (r - l) / 2; // 防止越界
        if (sum[middle] > target) r = middle;
        else if (sum[middle] < target) l = middle + 1;
        else if (sum[middle] == target) return middle;
    }
    return -1;
}

int main() {
    long M;
    scanf("%ld", &M);
    long long *sum = (long long *) malloc(sizeof(long long) * (M+1));
    sum[0] = 0;
    for (int i = 1; i <= M; i++) sum[i] = sum[i - 1] + i;
    for (int i = 1; i <= M; i++) {
        int bound = lower_bound(sum, i, M, M + sum[i - 1]);
        if (bound != -1)
            printf("%ld %ld\n", i, bound);
    }
    return 0;
}

2. 差分

一般地，差分主要用于让一个序列某一特定范围内的所有值都加上或减去一个常数。

直接说比较抽象，我们也是先从问题出发引出差分，现在给定一个数组q[8] = {1, 2, 5, 3, 7, 9, 4, 5 }，现在需要对这个数组对相应区间中的所有数加上或减去一个值，执行该操作多次，最后返回数组的最终状况。例如：[3, 5]区间中所有元素加10，则将数组变为[1, 2, 5, 13, 17, 19, 4, 5 ]，[1, 4]区间中所有元素减3，则将数组变为[1, -1, 2, 10, 14, 19, 4, 5 ]。

直接遍历去减就行，但是如果要运算的区间较多呢，例如给出300次变化，那我们便要进行300次遍历。数组长度为n，变化次数为m，则时间复杂度为o(nm)。

接着我们引出差分，所谓差分，可以简单的看成序列中每个元素与其前一个元素的差。以给出的数组为例，d[8] = [1, 1, 3, -2, 4, 2, -5, -1]，这串数看起来似乎没什么意义，但是我们对它求一下前缀和就会发现sum_d[8] = [1, 2, 5, 3, 7, 9, 4, 5 ]即原数组。

在这个过程中如果我们对d中第二个元素加3，就会发现sum_d从第二位起所有元素都加了3，同样的如果对第五位元素减去3，那么从第五位起所有元素又都减了3，这样操作下来，相当于第二个到第四个元素都加了3，同理，如果我们想要实现区间[3, 5]中的元素均加10，只需让d[3] = d[3] + 10 , d[6] = d[6] - 10，最后会反映在sum_d中。即[L, R]所有元素加value只需d[L] = d[L] + value, d[R+1] = d[R+1] - value，最后求出数组d的前缀和即为变化后的数组。

接着我们可以发现，d只用来统计区间变化时的情况，所以我们实际上并不需要计算q的差分，d统一初始为0，记录区间的变化情况，求出sum_d后再加回到q上结果也是一样的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<stdio.h>
// 注意这里d需要多开一个数组，因为add时存在r+1，否则会有数组越界的情况
// 当然也可以不多开，在add里面判断是否为边界单独处理，但代价是每次调用add时都要判断是否越界
int d[9] = {0};

void add(int l, int r, int v) {
    d[l] += v;
    d[r + 1] -= v;
}

int main() {
    int q[8] = {1, 2, 5, 3, 7, 9, 4, 5};
    add(2, 4, 5);
    add(1, 3, 2);
    add(0, 2, -3);
    // 计算前缀和
    for (int i = 1; i < 8; i++) d[i] += d[i - 1];
    for (int i = 0; i < 8; i++) {
        q[i] += d[i];
        printf("%d ", q[i]);
    }
    return 0;
}

同样的，我们推广到二维，类比前缀和的二维，我们不会再进行详细的介绍，简单带过一下，先给出个例子我们再去具体介绍，二维数组如下：

1
2
3
4
5
6
int q[4][4] = {
    {2,  3,  23, 5},
    {6,  33, 7,  45},
    {23, 4,  9,  56},
    {34, 57, 78, 75},
};

区域[1, 1]~[3, 2]加3，区域[1, 2]~[2, 3]减5，最后给出变化后的数组。

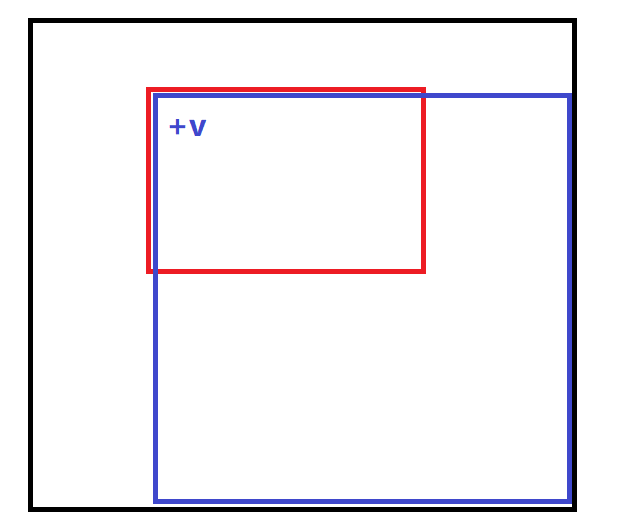
现在我们来看下图，如果我们要将红色区域+v，我们将x1,y1的差分数组+v，那它影响的区域为所有蓝色区域

image

所以我们需要修改的位置有：

  • d[x1][y1] + v
  • d[x1][y2+1] + v
  • d[x2+1][y1] + v
  • d[x2+1][y2+1] - v

image

接着我们来看代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<stdio.h>

const int n = 4;    // 行数
const int m = 4;    // 列数
int q[4][4] = {
        {2,  3,  23, 5},
        {6,  33, 7,  45},
        {23, 4,  9,  56},
        {34, 57, 78, 75},
};

int d[5][5];    // 多开一个长度防止越界
int sum[4][4];

void add(int x1, int y1, int x2, int y2, int v) {
    d[x1][y1] += v;
    d[x1][y2 + 1] -= v;
    d[x2 + 1][y1] -= v;
    d[x2 + 1][y2 + 1] += v;
}

void pre_sum() {
    sum[0][0] = d[0][0];
    for (int i = 1; i < n; i++) sum[i][0] = sum[i - 1][0] + d[i][0];
    for (int j = 1; j < m; j++) sum[0][j] = sum[0][j - 1] + d[0][j];
    for (int i = 1; i < n; i++)
        for (int j = 1; j < m; j++)
            sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + d[i][j];
}

int main() {
    add(1, 1, 3, 2, 3);
    add(1, 2, 2, 3, 5);
    pre_sum();  // 求出d的前缀和
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; ++j) {
            q[i][j] += sum[i][j];
            printf("%d ", q[i][j]);
        }
        printf("\n");
    }
    return 0;
}

例题1 统计奇数

题目

题目链接

长度为n的数组初始全为0，每分钟数组元素的值都会自增1。m次操作，每次选择一个区间，在自增的基础上额外增1，求m次操作后数组中奇数的个数。

示例：

1
2
3
4
// 输入
3,2,[1,2],[2,3]
// 输出
2

示例说明

1
2
第一分钟后 第一个数为2，第二个数为2，第三个数为1
第二分钟后 第一个数为3，第二个数为4，第三个数为3，一共两个数为奇数，所以输出2

其中：

  • 1 ≤ n ≤ 2*10^5
  • 1 ≤ m ≤ 2*10^5
  • 1 ≤ l[i] ≤ r[i] ≤ n

分析

需要注意的是按照题目的说法给出的区间[1,2]指的不是下表，而是第几个数，题目也比较简单，如果前面的部分看懂了这题没啥问题，简单练下手

1
2
3
4
5
6
7
8
9
10
11
12
static int d[200001], sum[200001];

int oddnumber(int n, int m, int *l, int lLen, int *r, int rLen) {
    for (int i = 0; i < m; i++)
        d[l[i]]++, d[r[i] + 1]--;
    for (int i = 1; i <= n; i++)
        sum[i] = sum[i - 1] + d[i];
    int Ans = 0;
    for (int i = 1; i <= n; i++)
        if ((sum[i] + m) % 2 == 1) Ans++;
    return Ans;
}

课后作业

题目链接

题目描述

在 n x n 的格子上有 m 个地毯。

给出这些地毯的信息，问每个点被多少个地毯覆盖。

输入格式

第一行，两个正整数 n,m。意义如题所述。

接下来 m 行，每行两个坐标 (x_1,y_1) 和 (x_2,y_2)，代表一块地毯，左上角是 (x_1,y_1)，右下角是 (x_2,y_2)。

输出格式

输出 n 行，每行 n 个正整数。

第 i 行第 j 列的正整数表示 (i,j) 这个格子被多少个地毯覆盖。

样例

样例输入

1
2
3
4
5 3
2 2 3 3
3 3 5 5
1 2 1 4

样例输出

1
2
3
4
5
0 1 1 1 0
0 1 1 0 0
0 1 2 1 1
0 0 1 1 1
0 0 1 1 1

样例解释

覆盖第一个地毯后：

0 0 0 0 0
0 1 1 0 0
0 1 1 0 0
0 0 0 0 0
0 0 0 0 0

覆盖第一、二个地毯后：

0 0 0 0 0
0 1 1 0 0
0 1 2 1 1
0 0 1 1 1
0 0 1 1 1

覆盖所有地毯后：

0 1 1 1 0
0 1 1 0 0
0 1 2 1 1
0 0 1 1 1
0 0 1 1 1

数据范围

对于 20% 的数据，有 n < 50，m < 100。

对于 100% 的数据，有 n,m < 1000。

作业答案

典型的二维差分，需要注意的点还是：

  1. 注意数组越界，将特殊情况单独进行讨论
  2. 区间指的不是下表，而是第几个数
  3. malloc为d开辟空间后需要初始化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include<stdio.h>
#include<malloc.h>
#include<string.h>

void add(int x1, int y1, int x2, int y2, int **d) {
    d[x1][y1] += 1;
    d[x1][y2 + 1] -= 1;
    d[x2 + 1][y1] -= 1;
    d[x2 + 1][y2 + 1] += 1;
}

void pre_sum(int numsSize, int **d, int **sum) {
    sum[0][0] = d[0][0];
    for (int i = 1; i < numsSize; i++) sum[i][0] = sum[i - 1][0] + d[i][0];
    for (int j = 1; j < numsSize; j++) sum[0][j] = sum[0][j - 1] + d[0][j];
    for (int i = 1; i < numsSize; i++)
        for (int j = 1; j < numsSize; j++)
            sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + d[i][j];
}


int main() {
    int n, m;
    scanf("%d %d", &n, &m);

    int **d = (int **) malloc(sizeof(int *) * (n + 1));
    for (int i = 0; i < n + 1; ++i) {
        d[i] = (int *) malloc(sizeof(int) * (n + 1));
        memset(d[i], 0, sizeof(int) * (n + 1));
    }

    int **sum = (int **) malloc(sizeof(int *) * n);
    for (int i = 0; i < n; i++)
        sum[i] = (int *) malloc(sizeof(int) * n);

    while (m--) {
        int x1, x2, y1, y2;
        scanf("%d %d %d %d", &x1, &y1, &x2, &y2);
        add(x1 - 1, y1 - 1, x2 - 1, y2 - 1, d);
    }

    pre_sum(n, d, sum);  // 求出d的前缀和

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++)
            printf("%d ", sum[i][j]);
        printf("\n");
    }

    return 0;
}

3. 双指针

通过题目我们可以更加直观的了解，会在题目分析中进行详细解释，在此先不做介绍。

例题1 移除元素

题目

题目链接

给你一个数组 nums 和一个值 val，你需要原地移除所有数值等于 val 的元素，并返回移除后数组的新长度。
不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并原地修改输入数组。
元素的顺序可以改变。
不需要考虑数组中超出新长度后面的元素。

示例 1：
输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]
解释：函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。例如，函数返回的新长度为 2 ，而 nums = [2,2,3,3] 或 nums = [2,2,0,0]，也会被视作正确答案。

示例 2：
输入：nums = [0,1,2,2,3,0,4,2], val = 2
输出：5, nums = [0,1,4,0,3]
解释：函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。你不需要考虑数组中超出新长度后面的元素。

其中：

  • 0 <= nums.length <= 100
  • 0 <= nums[i] <= 50
  • 0 <= val <= 100

分析

通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。

定义快慢指针

  • 快指针：寻找新数组的元素 ，新数组就是不含有目标元素的数组
  • 慢指针：指向更新 新数组下标的位置

第一个指针（快指针）负责遍历，第二个指针（慢指针）负责接收第一个指针指向的不是删除元素的值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 时间复杂度：O(n)
// 空间复杂度：O(1)
int removeElement(int *nums, int numsSize, int val)
{
    int slowIndex = 0;
    for (int fastIndex = 0; fastIndex < numsSize; fastIndex++)
    {
        if (val != nums[fastIndex])
        {
            nums[slowIndex++] = nums[fastIndex];
        }
    }
    return slowIndex;
}

相向双指针方法：基于元素顺序可以改变的题目描述改变了元素相对位置，确保了移动最少元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 时间复杂度：O(n)
// 空间复杂度：O(1)
int removeElement(int *nums, int numsSize, int val)
{
        int leftIndex = 0;
        int rightIndex = numsSize - 1;
        while (leftIndex <= rightIndex) {
            // 找左边等于val的元素
            while (leftIndex <= rightIndex && nums[leftIndex] != val){
                ++leftIndex;
            }
            // 找右边不等于val的元素
            while (leftIndex <= rightIndex && nums[rightIndex] == val) {
                -- rightIndex;
            }
            // 将右边不等于val的元素覆盖左边等于val的元素
            if (leftIndex < rightIndex) {
                nums[leftIndex++] = nums[rightIndex--];
            }
        }
        return leftIndex;   // leftIndex一定指向了最终数组末尾的下一个元素
}

课后作业

作业一

题目链接

给定 s 和 t 两个字符串，当它们分别被输入到空白的文本编辑器后，如果两者相等，返回 true 。# 代表退格字符。
注意：如果对空文本输入退格字符，文本继续为空。
【附加要求：不能使用额外空间】

示例 1：
输入：s = “ab#c”, t = “ad#c”
输出：true
解释：s 和 t 都会变成 “ac”。

示例 2：
输入：s = “ab##”, t = “c#d#”
输出：true
解释：s 和 t 都会变成 “”。

示例 3：
输入：s = “a#c”, t = “b”
输出：false
解释：s 会变成 “c”，但 t 仍然是 “b”。

其中：

  • 1 <= s.length, t.length <= 200
  • s 和 t 只含有小写字母以及字符 '#'

作业二

题目链接

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。
要求时间复杂度为O(n)

示例 1：
输入：nums = [-4,-1,0,3,10]
输出：[0,1,9,16,100]
解释：平方后，数组变为 [16,1,0,9,100]
排序后，数组变为 [0,1,9,16,100]

示例 2：
输入：nums = [-7,-3,2,3,11]
输出：[4,9,9,49,121]

其中：

  • 1 <= nums.length <= 十的四次方
  • 负十的四次方<= nums[i] <= 十的四次方
  • nums 已按 非递减顺序 排序

作业答案

作业一

一个字符是否会被删掉，只取决于该字符后面的退格符，而与该字符前面的退格符无关。因此当我们逆序地遍历字符串，就可以立即确定当前字符是否会被删掉。

具体地，我们定义 skip 表示当前待删除的字符的数量。每次我们遍历到一个字符：

  • 若该字符为退格符，则我们需要多删除一个普通字符，我们让 skip 加 1
  • 若该字符为普通字符
  • 若 skip 为 0，则说明当前字符不需要删去
  • 若 skip 不为 0，则说明当前字符需要删去，我们让 skip 减 1

这样，我们定义两个指针，分别指向两字符串的末尾。每次我们让两指针逆序地遍历两字符串，直到两字符串能够各自确定一个字符，然后将这两个字符进行比较。重复这一过程直到找到的两个字符不相等，或遍历完字符串为止。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
bool backspaceCompare(char* S, char* T) {
    int i = strlen(S) - 1, j = strlen(T) - 1;
    int skipS = 0, skipT = 0;

    while (i >= 0 || j >= 0) {
        while (i >= 0) {
            // 接收到字符或者S遍历结束时跳出循环
            if (S[i] == '#') {
                skipS++, i--;
            } else if (skipS > 0) {
                skipS--, i--;
            } else {
                break;
            }
        }
        while (j >= 0) {
            // 接收到字符或者T遍历结束时跳出循环
            if (T[j] == '#') {
                skipT++, j--;
            } else if (skipT > 0) {
                skipT--, j--;
            } else {
                break;
            }
        }
        if (i >= 0 && j >= 0) {
            // S和T均接收到了字符，进行比较
            if (S[i] != T[j]) {
                return false;
            }
        } else {
            // 至少一个字符串遍历结束，另一个遍历结束或者接收到了字符
            if (i >= 0 || j >= 0) {
                return false;
            }
        }
        i--, j--;
    }
    return true;
}

作业二

方法一：正数负数两侧分别平方，负数侧单调递减，正数侧单调递增，可以使用归并排序，学完排序模块回顾即可。

方法二：使用两个指针分别指向位置 0 和 n-1，每次比较两个指针对应的数，选择较大的那个逆序放入答案并移动指针。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int* sortedSquares(int* nums, int numsSize, int* returnSize) {
    int* ans = malloc(sizeof(int) * numsSize);
    *returnSize = numsSize;
    for (int i = 0, j = numsSize - 1, pos = numsSize - 1; i <= j;) {
        if (nums[i] * nums[i] > nums[j] * nums[j]) {
            ans[pos] = nums[i] * nums[i];
            ++i;
        } else {
            ans[pos] = nums[j] * nums[j];
            --j;
        }
        --pos;
    }
    return ans;
}

4. 滑动窗口

例题1 长度最小的子数组

题目

题目链接

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

要求时间复杂度不超过O(nlogn)

示例 1：
输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：
输入：target = 4, nums = [1,4,4]
输出：1

示例 3：
输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

其中：

  • 1 <= target <= 十的九次方
  • 1 <= nums.length <= 十的五次方
  • 1 <= nums[i] <= 十的五次方

分析

接下来就开始介绍数组操作中另一个重要的方法：滑动窗口。

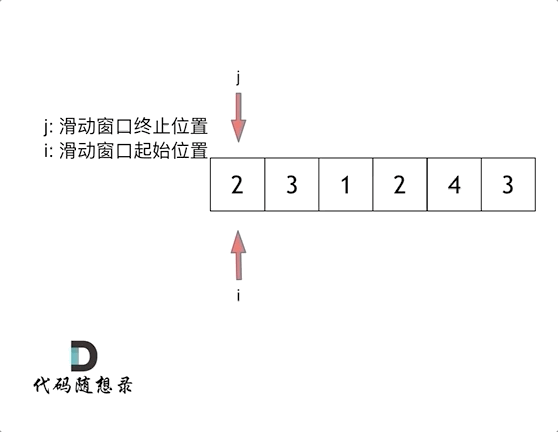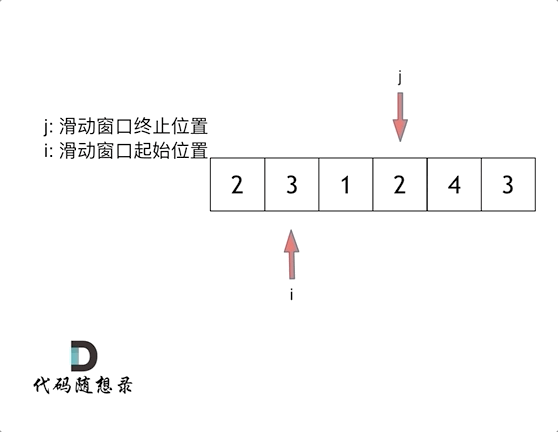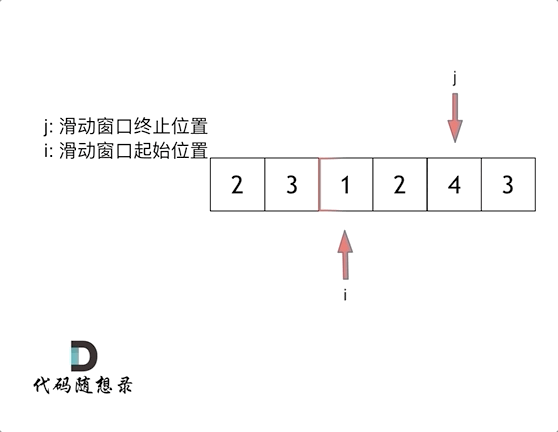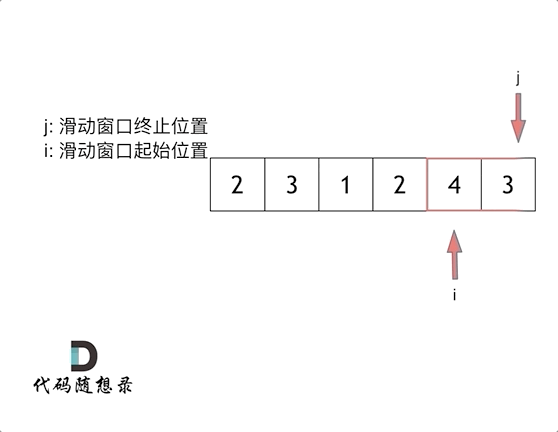
所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

这里还是以题目中的示例来举例，s=7， 数组是 2，3，1，2，4，3，来看一下查找的过程：
image
最后找到 4，3 是最短距离。

其实从动画中可以发现滑动窗口也可以理解为双指针法的一种！只不过这种解法更像是一个窗口的移动，所以叫做滑动窗口更适合一些。

在本题中实现滑动窗口，主要确定如下三点：

  • 窗口内是什么？
  • 如何移动窗口的起始位置？
  • 如何移动窗口的结束位置？

窗口就是满足其和 ≥ s 的长度最小的 连续 子数组。
窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。
窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，窗口的起始位置设置为数组的起始位置就可以了。

滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int minSubArrayLen(int target, int *nums, int numsSize)
{
    int result = INT_MAX;
    int sum = 0;         // 滑动窗口数值之和
    int i = 0;           // 滑动窗口起始位置
    int subLength = 0;   // 滑动窗口的长度
    for (int j = 0; j < numsSize; j++)
    {
        sum += nums[j];
        // 注意这里使用while，每次更新 i（起始位置），并不断比较子序列是否符合条件
        while (sum >= target)
        {
            subLength = (j - i + 1); // 取子序列的长度
            result = result < subLength ? result : subLength;
            sum -= nums[i++]; // 这里体现出滑动窗口的精髓之处，不断变更i（子序列的起始位置）
        }
    }
    // 如果result没有被赋值的话，就返回0，说明没有符合条件的子序列
    return result == INT_MAX ? 0 : result;
}

课后作业

题目

题目链接

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。要求在o(n) 时间内解决此问题。

注意：

  • 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
  • 如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：
输入：s = “ADOBECODEBANC”, t = “ABC”
输出：”BANC”

示例 2：
输入：s = “a”, t = “a”
输出：”a”

示例 3:
输入: s = “a”, t = “aa”
输出: “”
解释: t 中两个字符 ‘a’ 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

其中：

  • 1 <= s.length, t.length <= 10^5
  • s 和 t 由英文字母组成

说明

这道题虽然标的是困难但实际上没那么难，都是同一题型，对于C++、Java哈希表直接用就行，C的话需要我们自己构造一下，关于哈希表的详细知识会在”查找“模块中进行详细解释，感兴趣的同学也可先行了解

作业答案

分析

采用滑动窗口解决该问题。

我们可以先记录t中字母的种类以及各字母需要的数量，显然，外层循环条件为右侧指针小于s的长度，在右侧指针推进时我们可以判断这个字母是否已经让满足数量，记录窗口中字母满足的个数，如果满足个数与t中的字母种类数相同，证明已达到要求，开始让左侧指针进行移动，减小字符串长度，直到不再满足要求。循环执行下去，就可得到我们想要的结果。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71

char *minWindow(char *s, char *t)
{
    int lent = strlen(t), lens = strlen(s);

    int len = lens + 1; //用来判断可能会出现的找不到的情况，因为找到的话那字符串总长不会超过lens

    int *need = (int *)malloc(sizeof(int) * 128); //字符串T中的字母种类和个数，用字母ASCII码做下标，值作为个数
    memset(need, 0, sizeof(int) * 128);
    int *window = (int *)malloc(sizeof(int) * 128); //滑动窗口中包含的字母种类和个数，规则同need
    memset(window, 0, sizeof(int) * 128);

    int left = 0, right = 0; //窗的左右边界，这是一个左闭右开的窗
    int cnt = 0;    //字符串T中的字母种类
    int valid = 0; //窗口中满足字符串T中的字母种类，比如字符串T中有字母a共10个，那么窗口中有10个a的时候这个值++
    int start = 0;

    //记录字符串T
    for (int i = 0; i < lent; i++)
    {
        need[t[i]]++;
    }

    for (int i = 0; i < 128; i++)
    { //字符串T中字母种类
        if (need[i] != 0)
        {
            cnt++;
        }
    }

    while (right < lens) //边界条件
    {
        char c = s[right]; //将要移入窗口的字符
        right++;           //扩窗
        if (need[c] != 0)
        { //窗口数据更新
            window[c]++;
            if (window[c] == need[c])
            {
                valid++;
            }
        }
        while (valid == cnt)
        { //判断左侧窗口是否要收缩
            if (right - left < len)
            { //更新最小覆盖子串
                start = left;
                len = right - left;
            }
            char d = s[left]; //将要移出窗口的字符
            left++;           //缩窗
            if (need[d] != 0)
            {
                if (window[d] == need[d])
                {
                    valid--;
                }
                window[d]--;
            }
        }
    }
    if (len != lens + 1)
    { //返回最小覆盖子串
        char *res = (char *)malloc(sizeof(char) * (len + 1));
        *res = '\0';
        strncat(res, s + start, len);
        return res;
    }
    return "";
}

5. 螺旋矩阵

例题1 螺旋矩阵Ⅱ

题目

题目链接

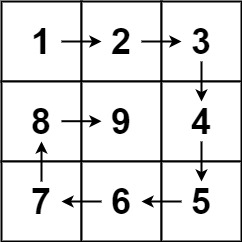
给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

image

示例 1：

1
2
输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

1
2
输入：n = 1
输出：[[1]]

其中：1<= n <=20

分析

本体不涉及具体的算法，但是对过程的分析能力较为考察。
如果不先对题目进行分析直接判断最后很可能造成混乱。

当n为奇数时，最后会剩下单独的一个数，这个数我们最后单独处理，总共需要走n/2圈（奇数向下取整）
当n为偶数时，总共需要走n/2圈
我们可以写为定义loop为n/2，外层循环写为while(loop--)，接着用4次循环进行右下左上的遍历，为保持统一性，我们输出时采用左闭右开。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
int **generateMatrix(int n, int *returnSize, int **returnColumnSizes)
{
    int startx = 0, starty = 0; // 定义每循环一个圈的起始位置
    int loop = n / 2;           // 每个圈循环几次，例如n为奇数3，那么loop = 1 只是循环一圈，矩阵中间的值需要单独处理
    int count = 1;              // 用来给矩阵中每一个空格赋值
    int offset = 1;             // 每一圈循环，需要控制每一条边遍历的长度
    int i, j;
    *returnSize = n;
    *returnColumnSizes = (int *)malloc(sizeof(int) * n);
    int **res = (int **)malloc(sizeof(int *) * n);
    for (i = 0; i < n; i++)
    {
        res[i] = (int *)malloc(sizeof(int) * n);
        (*returnColumnSizes)[i] = n;
    }
    while (loop--)
    {
        i = startx;
        j = starty;

        // 下面开始的四个for就是模拟转了一圈
        // 模拟填充上行从左到右(左闭右开)
        for (j = starty; j < starty + n - offset; j++)
        {
            res[startx][j] = count++;
        }
        // 模拟填充右列从上到下(左闭右开)
        for (i = startx; i < startx + n - offset; i++)
        {
            res[i][j] = count++;
        }
        // 模拟填充下行从右到左(左闭右开)
        for (; j > starty; j--)
        {
            res[i][j] = count++;
        }
        // 模拟填充左列从下到上(左闭右开)
        for (; i > startx; i--)
        {
            res[i][j] = count++;
        }

        // 第二圈开始的时候，起始位置要各自加1， 例如：第一圈起始位置是(0, 0)，第二圈起始位置是(1, 1)
        startx++;
        starty++;

        // offset 控制每一圈里每一条边遍历的长度
        offset += 2;
    }

    // 如果n为奇数的话，需要单独给矩阵最中间的位置赋值
    if (n % 2)
    {
        res[n / 2][n / 2] = count;
    }
    return res;
}

课后作业

题目

题目链接

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

其中：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= m, n <= 10
  • -100 <= matrix[i][j] <= 100

答案

这题跟例题差不多，把正方形换成了矩形，过程倒了过来，作为一个巩固练习，在此不多赘述。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
int* spiralOrder(int** matrix, int matrixSize, int* matrixColSize, int* returnSize) {
    if (matrixSize == 0 || matrixColSize[0] == 0) {
        *returnSize = 0;
        return NULL;
    }

    int rows = matrixSize, columns = matrixColSize[0];
    int total = rows * columns;
    int* order = malloc(sizeof(int) * total);
    *returnSize = 0;

    int left = 0, right = columns - 1, top = 0, bottom = rows - 1;
    while (left <= right && top <= bottom) {
        for (int column = left; column <= right; column++) {
            order[(*returnSize)++] = matrix[top][column];
        }
        for (int row = top + 1; row <= bottom; row++) {
            order[(*returnSize)++] = matrix[row][right];
        }
        if (left < right && top < bottom) {
            for (int column = right - 1; column > left; column--) {
                order[(*returnSize)++] = matrix[bottom][column];
            }
            for (int row = bottom; row > top; row--) {
                order[(*returnSize)++] = matrix[row][left];
            }
        }
        left++;
        right--;
        top++;
        bottom--;
    }
    return order;
}

附加题 二分查找

二分查找作为程序员的一项基本技能，是面试官最常使用来考察程序员基本素质的算法之一，也是解决很多查找类题目的常用方法，它可以达到O(log n)的时间复杂度。

一般在出现以下特性时考虑二分查找

  1. 待查找的数组有序或者部分有序
  2. 要求时间复杂度低于O(n)，或者直接要求时间复杂度为O(log n)

需要注意的是一旦数据中有重复元素，使用二分查找法返回的元素下标可能不是唯一的

二分查找最重要的便是确定不变量，在二分查找中区间的定义便是不变量，在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)，下面将分别进行展开。

写法一

我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] 。

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

  • while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
  • if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle + 1

写法二

如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。

  • while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
  • if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]
  • if (nums[middle] < target) left 更新为 middle + 1，因为左侧与右侧不同，是闭区间，因为当前这个nums[middle]一定不是target，直接指向middle + 1即可

例题1 搜索插入位置

题目

题目链接

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

其中：

  • 1 <= nums.length <= 10^4
  • -10^4 <= nums[i] <= 10^4
  • nums 为 无重复元素 的 升序 排列数组
  • -10^4 <= target <= 10^4

分析

数组已排序、时间复杂度为 O(log n) ，我们首先可以考虑二分查找

区间类型的话我们可以选用闭区间（其他区间不再举例），也就是说循环可以写为while (left < right)，当目标值与nums[middle]不相等时，根据情况将right设置为middle - 1，或left设置为middle + 1即可。

找到数字时返回索引：此时middle的值即为目标值索引
未找到数字时返回要插入的位置：此时high或low即为需要插入的位置

最后注意一个小细节，left、right都是很大的数，计算middle的过程中，二者相加可能会溢出，造成除以二之后的值并不是我们想要的。所以我们可以将middle = (left + right)/2; 修改为middle = left + ((right - left) / 2);。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int searchInsert(int* nums, int numsSize, int target){
    int right=numsSize-1,left=0,middle;
    while(left<=right){
        middle = left + ((right - left) / 2);
        if(nums[middle]==target){
            return middle;
        } else if( nums[middle]<target){
            left = middle + 1;
        } else {
            right = middle -1;
        }
    }
    return left;
}

例题2 在排序数组中查找元素的第一个和最后一个位置

题目

题目链接

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1
输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2
输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3
输入：nums = [], target = 0
输出：[-1,-1]

其中：

  • 0 <= nums.length <= 10^5
  • -10^9<= nums[i] <= 10^9
  • nums 是一个非递减数组
  • -10^9 <= target <= 10^9

分析

数组已排序、时间复杂度为 O(log n) ，先考虑二分查找，但是这题看着容易但实现起来细节方面还是比较绕的，我们首先把情况分析一下：

  • 情况一：target 在数组范围的右边或者左边，例如数组{3, 4, 5}，target为2或者数组{3, 4, 5}，target为6，此时应该返回{-1, -1}
  • 情况二：target 在数组范围中，且数组中不存在target，例如数组{3,6,7}，target为5，此时应该返回{-1, -1}
  • 情况三：target 在数组范围中，且数组中存在target，例如数组{3,6,7}，target为6，此时应该返回{1, 1}

而我们的目标是左右边界两个

寻找右边界

寻找target的右边界（不包括target），记为rightBorder
区间选用闭区间，即循环写为while (left <= right)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 如果rightBorder为没有被赋值（即target在数组范围的左边，例如数组[3,3]，target为2），为了处理情况一
int getRightBorder(int *nums, int numsSize, int target) {
    // 定义target在左闭右闭的区间里，[left, right]
    int left = 0, right = numsSize - 1; 
    int rightBorder = -2; // 记录rightBorder没有被赋值的情况
    while (left <= right) { // 当left==right，区间[left, right]依然有效
        int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
        if (nums[middle] > target) {
            right = middle - 1; // target 在左区间，所以[left, middle - 1]
        } else { // 当nums[middle] == target的时候，更新left，这样才能得到target的右边界
            left = middle + 1;
            rightBorder = left;
        }
    }
    // 情况一，这些数都比target大，返回-2
    // 情况二，位于中间，但是没有target，由于rightBorder每次都是middle + 1跟进，最后的值是插入位置右侧的数
    // 情况三，如果找到了，这里就是目标值的右侧一个数
    return rightBorder;	
}

寻找左边界

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// 二分查找，寻找target的左边界leftBorder（不包括target）
// 如果leftBorder没有被赋值（即target在数组范围的右边，例如数组[3,3],target为4），为了处理情况一
int getLeftBorder(int *nums, int numsSize, int target) {
    int left = 0;
    int right = numsSize - 1; // 定义target在左闭右闭的区间里，[left, right]
    int leftBorder = -2; // 记录一下leftBorder没有被赋值的情况
    while (left <= right) {
        int middle = left + ((right - left) / 2);
        if (nums[middle] >= target) { // 寻找左边界，就要在nums[middle] == target的时候更新right
            right = middle - 1;
            leftBorder = right;
        } else {
            left = middle + 1;
        }
    }
    // 情况一，这些数都比target小，返回-2
    // 情况二，位于中间，但是没有target，由于leftBorder每次都是middle - 1跟进，最后的值是插入位置左侧的数
    // 情况三，如果找到了，这里就是目标值的左侧一个数
    return leftBorder;
}

处理三中情况

  • 二者中有一个为-2，代表处于情况一，返回[-1,-1]即可
  • rightBorder - leftBorder > 1 代表情况三，这个数存在返回[ leftBorder + 1, rightBorder - 1 ] 即可
  • 剩余为情况二，返回[-1,-1]即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int *searchRange(int *nums, int numsSize, int target, int *returnSize)
{	// 为了直观一些写的比较啰嗦
    int leftBorder = getLeftBorder(nums, numsSize, target);
    int rightBorder = getRightBorder(nums, numsSize, target);
    int *answer = malloc(sizeof(int) * 2);

    if (leftBorder == -2 || rightBorder == -2)
    {
        answer[0] = -1;
        answer[1] = -1;
    }
    else if (rightBorder - leftBorder > 1)
    {
        answer[0] = leftBorder + 1;
        answer[1] = rightBorder - 1;
    }
    else
    {
        answer[0] = -1;
        answer[1] = -1;
    }
    *returnSize = 2;
    return answer;
}

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include<malloc.h>

int *searchRange(int *nums, int numsSize, int target, int *returnSize)
{
    int leftBorder = getLeftBorder(nums, numsSize, target);
    int rightBorder = getRightBorder(nums, numsSize, target);
    int *answer = malloc(sizeof(int) * 2);

    if (leftBorder == -2 || rightBorder == -2)
    {
        answer[0] = -1;
        answer[1] = -1;
    }
    else if (rightBorder - leftBorder > 1)
    {
        answer[0] = leftBorder + 1;
        answer[1] = rightBorder - 1;
    }
    else
    {
        answer[0] = -1;
        answer[1] = -1;
    }
    *returnSize = 2;
    return answer;
}

int getLeftBorder(int *nums, int numsSize, int target)
{
    int left = 0;
    int right = numsSize - 1; // 定义target在左闭右闭的区间里，[left, right]
    int leftBorder = -2;      // 记录一下leftBorder没有被赋值的情况
    while (left <= right)
    {
        int middle = left + ((right - left) / 2);
        if (nums[middle] >= target)
        { // 寻找左边界，就要在nums[middle] == target的时候更新right
            right = middle - 1;
            leftBorder = right;
        }
        else
        {
            left = middle + 1;
        }
    }
    return leftBorder;
}

int getRightBorder(int *nums, int numsSize, int target)
{
    // 定义target在左闭右闭的区间里，[left, right]
    int left = 0, right = numsSize - 1;
    int rightBorder = -2; // 记录rightBorder没有被赋值的情况
    while (left <= right)
    {                                             // 当left==right，区间[left, right]依然有效
        int middle = left + ((right - left) / 2); // 防止溢出 等同于(left + right)/2
        if (nums[middle] > target)
        {
            right = middle - 1; // target 在左区间，所以[left, middle - 1]
        }
        else
        { // 当nums[middle] == target的时候，更新left，这样才能得到target的右边界
            left = middle + 1;
            rightBorder = left;
        }
    }
    // 情况一，这些数都比target大，返回-2
    // 情况二，位于中间，但是没有target，由于rightBorder每次都是middle + 1跟进，最后的值是插入位置右侧的数
    // 情况三，如果找到了，这里就是目标值的右侧一个数
    return rightBorder;
}

课后作业

题目

题目链接

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。
由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。
注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

示例 1：
输入：x = 4
输出：2

示例 2：
输入：x = 8
输出：2
解释：8 的算术平方根是 2.82842…, 由于返回类型是整数，小数部分将被舍去。

其中：0 <= x <= 2^31 - 1

作业答案

采用二分查找，下界为1上界为x，比较中间元素的平方与x的大小关系，逐步缩小范围，没有太大难度，简单练习一下二分查找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int mySqrt(int x)
{
    int l = 0, r = x, ans = -1;
    while (l <= r)
    {
        int mid = l + (r - l) / 2;
        if ((long long)mid * mid <= x)
        {
            ans = mid;
            l = mid + 1;
        }
        else
        {
            r = mid - 1;
        }
    }
    return ans;
}
  • 时间复杂度：O(log x)，即为二分查找需要的次数。
  • 空间复杂度：O(1)。
 评论
评论插件加载失败
正在加载评论插件
  1. 1. 数组
    1. 1.1. 1. 前缀和
      1. 1.1.1. 例题1 长度最小的子数组
        1. 1.1.1.1. 题目
        2. 1.1.1.2. 分析
        3. 1.1.1.3. 代码
      2. 1.1.2. 课后作业
      3. 1.1.3. 作业答案
    2. 1.2. 2. 差分
      1. 1.2.1. 例题1 统计奇数
        1. 1.2.1.1. 题目
        2. 1.2.1.2. 分析
      2. 1.2.2. 课后作业
        1. 1.2.2.1. 题目描述
        2. 1.2.2.2. 输入格式
        3. 1.2.2.3. 输出格式
        4. 1.2.2.4. 样例
        5. 1.2.2.5. 数据范围
      3. 1.2.3. 作业答案
    3. 1.3. 3. 双指针
      1. 1.3.1. 例题1 移除元素
        1. 1.3.1.1. 题目
        2. 1.3.1.2. 分析
      2. 1.3.2. 课后作业
        1. 1.3.2.1. 作业一
        2. 1.3.2.2. 作业二
      3. 1.3.3. 作业答案
        1. 1.3.3.1. 作业一
        2. 1.3.3.2. 作业二
    4. 1.4. 4. 滑动窗口
      1. 1.4.1. 例题1 长度最小的子数组
        1. 1.4.1.1. 题目
        2. 1.4.1.2. 分析
        3. 1.4.1.3. 代码
      2. 1.4.2. 课后作业
        1. 1.4.2.1. 题目
        2. 1.4.2.2. 说明
      3. 1.4.3. 作业答案
        1. 1.4.3.1. 分析
        2. 1.4.3.2. 代码
    5. 1.5. 5. 螺旋矩阵
      1. 1.5.1. 例题1 螺旋矩阵Ⅱ
        1. 1.5.1.1. 题目
        2. 1.5.1.2. 分析
        3. 1.5.1.3. 代码
      2. 1.5.2. 课后作业
        1. 1.5.2.1. 题目
        2. 1.5.2.2. 答案
    6. 1.6. 附加题 二分查找
      1. 1.6.1. 写法一
      2. 1.6.2. 写法二
      3. 1.6.3. 例题1 搜索插入位置
        1. 1.6.3.1. 题目
        2. 1.6.3.2. 分析
        3. 1.6.3.3. 代码
      4. 1.6.4. 例题2 在排序数组中查找元素的第一个和最后一个位置
        1. 1.6.4.1. 题目
        2. 1.6.4.2. 分析
        3. 1.6.4.3. 代码
      5. 1.6.5. 课后作业
        1. 1.6.5.1. 题目
      6. 1.6.6. 作业答案
  1. 1. 数组
    1. 1.1. 1. 前缀和
      1. 1.1.1. 例题1 长度最小的子数组
        1. 1.1.1.1. 题目
        2. 1.1.1.2. 分析
        3. 1.1.1.3. 代码
      2. 1.1.2. 课后作业
      3. 1.1.3. 作业答案
    2. 1.2. 2. 差分
      1. 1.2.1. 例题1 统计奇数
        1. 1.2.1.1. 题目
        2. 1.2.1.2. 分析
      2. 1.2.2. 课后作业
        1. 1.2.2.1. 题目描述
        2. 1.2.2.2. 输入格式
        3. 1.2.2.3. 输出格式
        4. 1.2.2.4. 样例
        5. 1.2.2.5. 数据范围
      3. 1.2.3. 作业答案
    3. 1.3. 3. 双指针
      1. 1.3.1. 例题1 移除元素
        1. 1.3.1.1. 题目
        2. 1.3.1.2. 分析
      2. 1.3.2. 课后作业
        1. 1.3.2.1. 作业一
        2. 1.3.2.2. 作业二
      3. 1.3.3. 作业答案
        1. 1.3.3.1. 作业一
        2. 1.3.3.2. 作业二
    4. 1.4. 4. 滑动窗口
      1. 1.4.1. 例题1 长度最小的子数组
        1. 1.4.1.1. 题目
        2. 1.4.1.2. 分析
        3. 1.4.1.3. 代码
      2. 1.4.2. 课后作业
        1. 1.4.2.1. 题目
        2. 1.4.2.2. 说明
      3. 1.4.3. 作业答案
        1. 1.4.3.1. 分析
        2. 1.4.3.2. 代码
    5. 1.5. 5. 螺旋矩阵
      1. 1.5.1. 例题1 螺旋矩阵Ⅱ
        1. 1.5.1.1. 题目
        2. 1.5.1.2. 分析
        3. 1.5.1.3. 代码
      2. 1.5.2. 课后作业
        1. 1.5.2.1. 题目
        2. 1.5.2.2. 答案
    6. 1.6. 附加题 二分查找
      1. 1.6.1. 写法一
      2. 1.6.2. 写法二
      3. 1.6.3. 例题1 搜索插入位置
        1. 1.6.3.1. 题目
        2. 1.6.3.2. 分析
        3. 1.6.3.3. 代码
      4. 1.6.4. 例题2 在排序数组中查找元素的第一个和最后一个位置
        1. 1.6.4.1. 题目
        2. 1.6.4.2. 分析
        3. 1.6.4.3. 代码
      5. 1.6.5. 课后作业
        1. 1.6.5.1. 题目
      6. 1.6.6. 作业答案