LSM树

前言

Google的三篇论文：GFS(2003年)、MapReduce(2004年)、BigTable(2006年)，为开源界在大数据领域带来了无数的灵感

其中在 “BigTable” 的论文中很多很酷的方面之一就是它所使用的文件组织方式，这个方法更一般的名字叫 Log Structured-Merge Tree

在面对亿级别之上的海量数据的存储和检索的场景下，我们选择的数据库通常都是各种强力的NoSQL，比如Hbase、Cassandra、Leveldb、RocksDB等等，这其中前两者是Apache下面的顶级开源项目数据库，后两者分别是Google和Facebook开源的数据库存储引擎。而这些强大的NoSQL数据库都有一个共性，就是其底层使用的数据结构，都是仿照“BigTable”中的文件组织方式来实现的，也就是LSM-Tree

LSM-Tree全称是Log Structured Merge Tree，是一种分层、有序、面向磁盘的数据结构，其核心思想是充分了利用了，磁盘批量的顺序写要远比随机写性能高出很多

围绕这一原理进行设计和优化，以此让写性能达到最优，正如我们普通的Log的写入方式，这种结构的写入，全部都是以Append的模式追加，不存在删除和修改。当然有得就有舍，这种结构虽然大大提升了数据的写入能力，却是以牺牲部分读取性能为代价，故此这种结构通常适合于写多读少的场景。

故LSM被设计来提供比传统的B+树或者ISAM更好的写操作吞吐量，通过消去随机的本地更新操作来达到这个目标。这里面最典型的例子就属于Kakfa了，把磁盘顺序写发挥到了极致，故而在大数据领域成为了互联网公司标配的分布式消息中间件组件。

虽然这种结构的写非常简单高效，但其缺点是对读取特别是随机读很不友好，这也是为什么日志通常用在下面的两种简单的场景：

数据是被整体访问的，大多数数据库的WAL（write ahead log）也称预写log，包括mysql的Binlog等
数据是通过文件的偏移量offset访问的，比如Kafka

想要支持更复杂和高效的读取，比如按key查询和按range查询，就得需要做一步的设计，这也是LSM-Tree结构，除了利用磁盘顺序写之外，还划分了内存+磁盘多层的合并结构的原因，正是基于这种结构再加上不同的优化实现，才造就了在这之上的各种独具特点的NoSQL数据库，如Hbase，Cassandra，Leveldb，RocksDB，MongoDB，TiDB等。

LSM介绍

LSM 算法的原理是什么？

LSM tree (log-structured merge-tree) 是一种对频繁写操作非常友好的数据结构，同时兼顾了查询效率。LSM tree 是许多 key-value 型或日志型数据库所依赖的核心数据结构，例如 BigTable、HBase、Cassandra、LevelDB、SQLite、Scylla、RocksDB 等。

LSM tree 之所以有效是基于以下事实：磁盘或内存的连续读写性能远高于随机读写性能，有时候这种差距可以达到三个数量级之高。这种现象不仅对传统的机械硬盘成立，对 SSD 硬盘也同样成立。

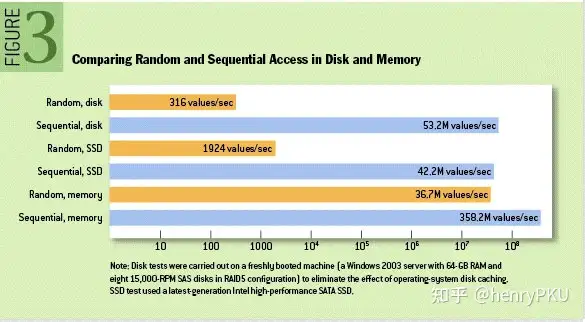
LSM tree 在工作过程中尽可能避免随机读写，充分发挥了磁盘连续读写的性能优势。

原理

SSTable

LSM tree 持久化到硬盘上之后的结构称为 Sorted Strings Table (SSTable)。顾名思义，SSTable 保存了排序后的数据（实际上是按照 key 排序的 key-value 对）。

每个 SSTable 可以包含多个存储数据的文件，称为 segment，每个 segment 内部都是有序的，但不同 segment 之间没有顺序关系。一个 segment 一旦生成便不再修改（immutable）。一个 SSTable 的示例如下：

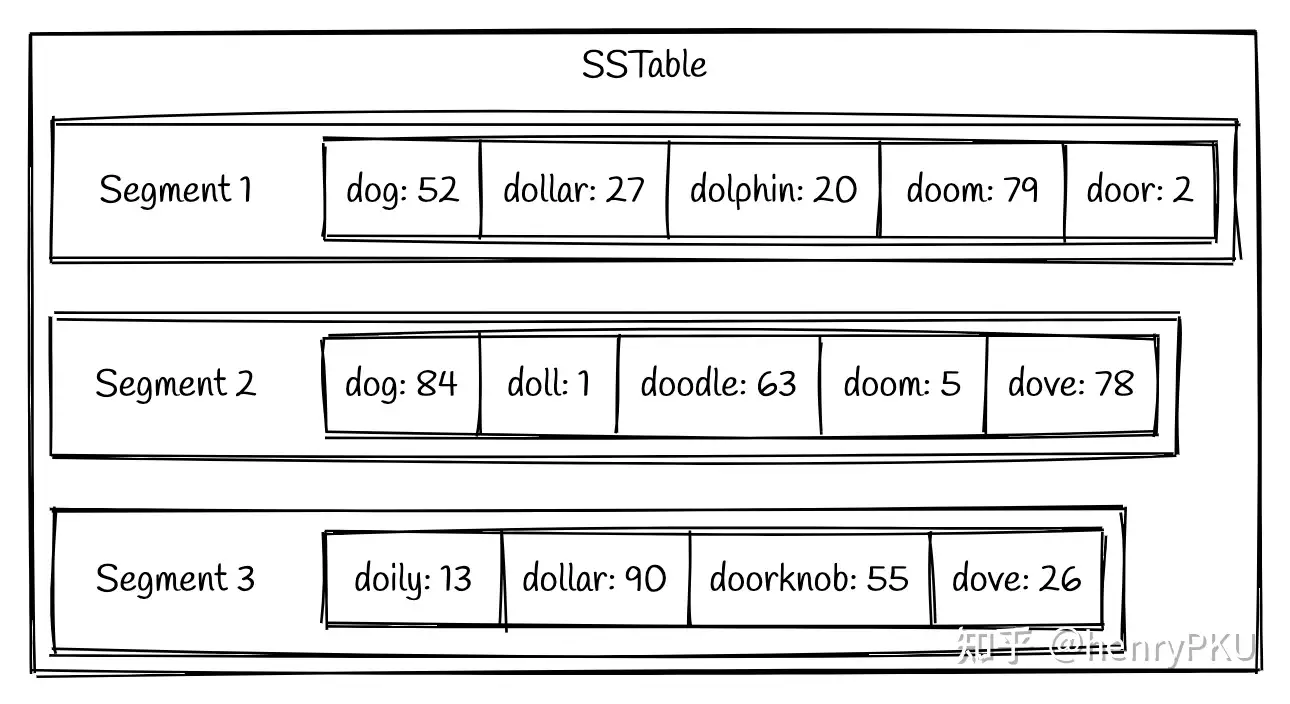
可以看到，每个 segment 内部的数据都是按照 key 排序的。下面我们来介绍每个 segment 是如何生成的。

写入LSM

LSM tree 的所有写操作均为连续写，因此效率非常高。但由于外部数据是无序到来的，如果无脑连续写入到 segment，显然是不能保证顺序的。

对此，LSM tree 会在内存中构造一个有序数据结构（称为 memtable），例如红黑树、跳表等（实践中总是采用跳表）。每条新到达的数据插入后，可以始终保持数据有序。

当写入的数据量达到一定阈值时，将触发有序结构的 flush 操作，把所有排好序的数据一次性写入到硬盘中（该过程为连续写），生成一个新的 segment。而之后有序结构便重新开始下一轮积攒数据的过程。

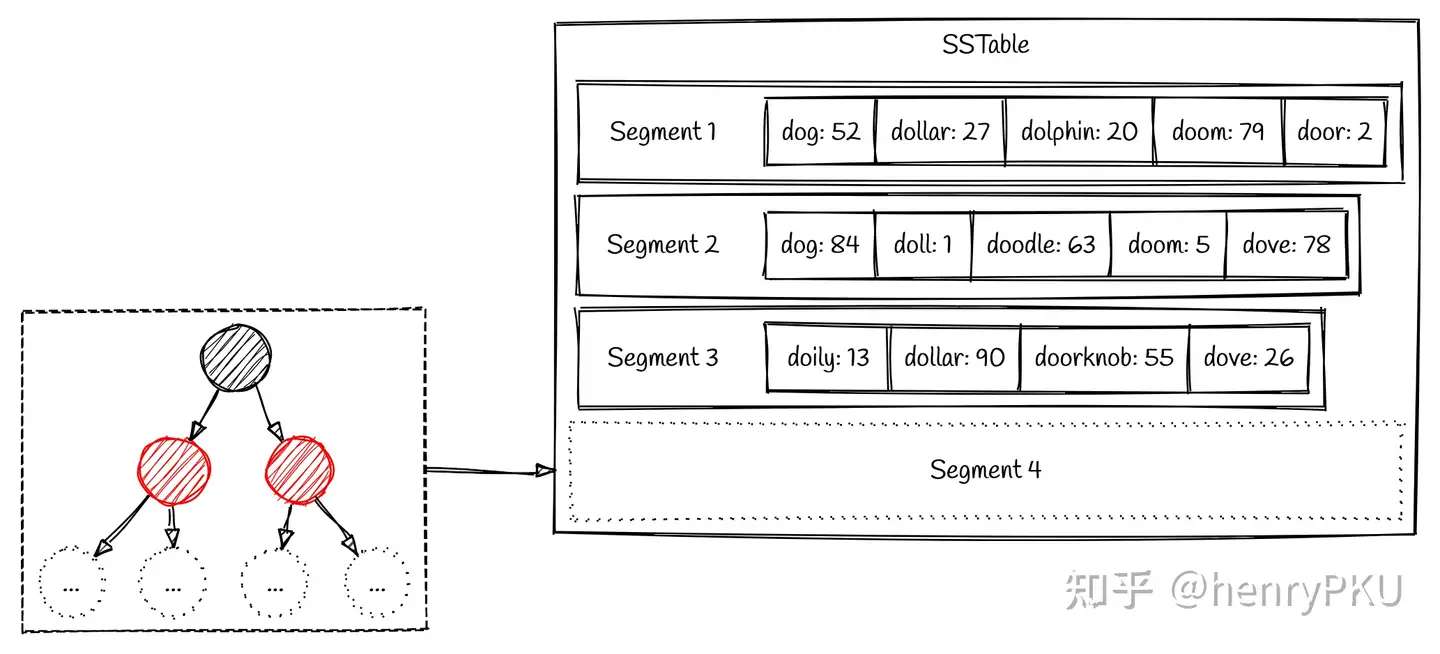
读取/查询数据

如何从 SSTable 中查询一条特定的数据呢？一个最简单直接的办法是扫描所有的 segment，直到找到所查询的 key 为止。通常应该从最新的 segment 扫描，依次到最老的 segment，这是因为越是最近的数据越可能被用户查询，把最近的数据优先扫描能够提高平均查询速度。

当扫描某个特定的 segment 时，由于该 segment 内部的数据是有序的，因此可以使用二分查找的方式，在 O(log⁡n) 的时间内得到查询结果。

但对于二分查找来说，要么一次性把数据全部读入内存，要么在每次二分时都消耗一次磁盘 IO，当 segment 非常大时（这种情况在大数据场景下司空见惯），这两种情况的代价都非常高。

一个简单的优化策略是，在内存中维护一个稀疏索引（sparse index），其结构如下图：

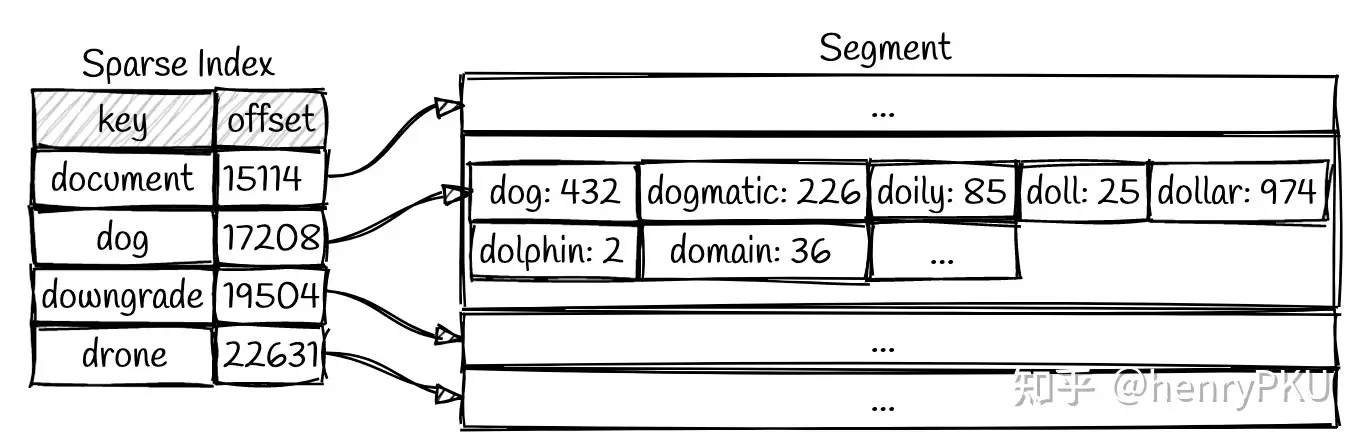
稀疏索引是指将有序数据切分成（固定大小的）块，仅对各个块开头的一条数据做索引。与之相对的是全量索引（dense index），即对全部数据编制索引，其中的任意一条数据发生增删均需要更新索引。

两者相比，全量索引的查询效率更高，达到了理论极限值 O(log⁡n) ，但写入和删除效率更低，因为每次数据增删时均需要因为更新索引而消耗一次 IO 操作。通常的关系型数据库，例如 MySQL 等，其内部采用 B tree 作为索引结构，这便是一种全量索引。

有了稀疏索引之后，可以先在索引表中使用二分查找快速定位某个 key 位于哪一小块数据中，然后仅从磁盘中读取这一块数据即可获得最终查询结果，此时加载的数据量仅仅是整个 segment 的一小部分，因此 IO 代价较小。

稀疏索引极大地提高了查询性能，然而有一种极端情况却会造成查询性能骤降：当要查询的结果在 SSTable 中不存在时，我们将不得不依次扫描完所有的 segment，这是最差的一种情况。

解决方案：布隆过滤器（bloom filter），布隆过滤器是一种空间效率极高的算法，能够快速地检测一条数据是否在数据集中存在。我们只需要在写入每条数据之前先在布隆过滤器中登记一下，在查询时即可断定某条数据是否缺失。

布隆过滤器的内部依赖于哈希算法，当布隆过滤器认为一条数据出现过，那么该条数据很可能出现过；但如果布隆过滤器认为一条数据没出现过，那么该条数据一定没出现过。

文件合并（Compaction）

随着数据的不断积累，SSTable 将会产生越来越多的 segment，导致查询时扫描文件的 IO 次数增多，效率降低，因此需要有一种机制来控制 segment 的数量。

对此，LSM tree 会定期执行文件合并（compaction）操作，将多个 segment 合并成一个较大的 segment，随后将旧的 segment 清理掉。由于每个 segment 内部的数据都是有序的，合并过程类似于归并排序，效率很高，只需要 O(n) 的时间复杂度。

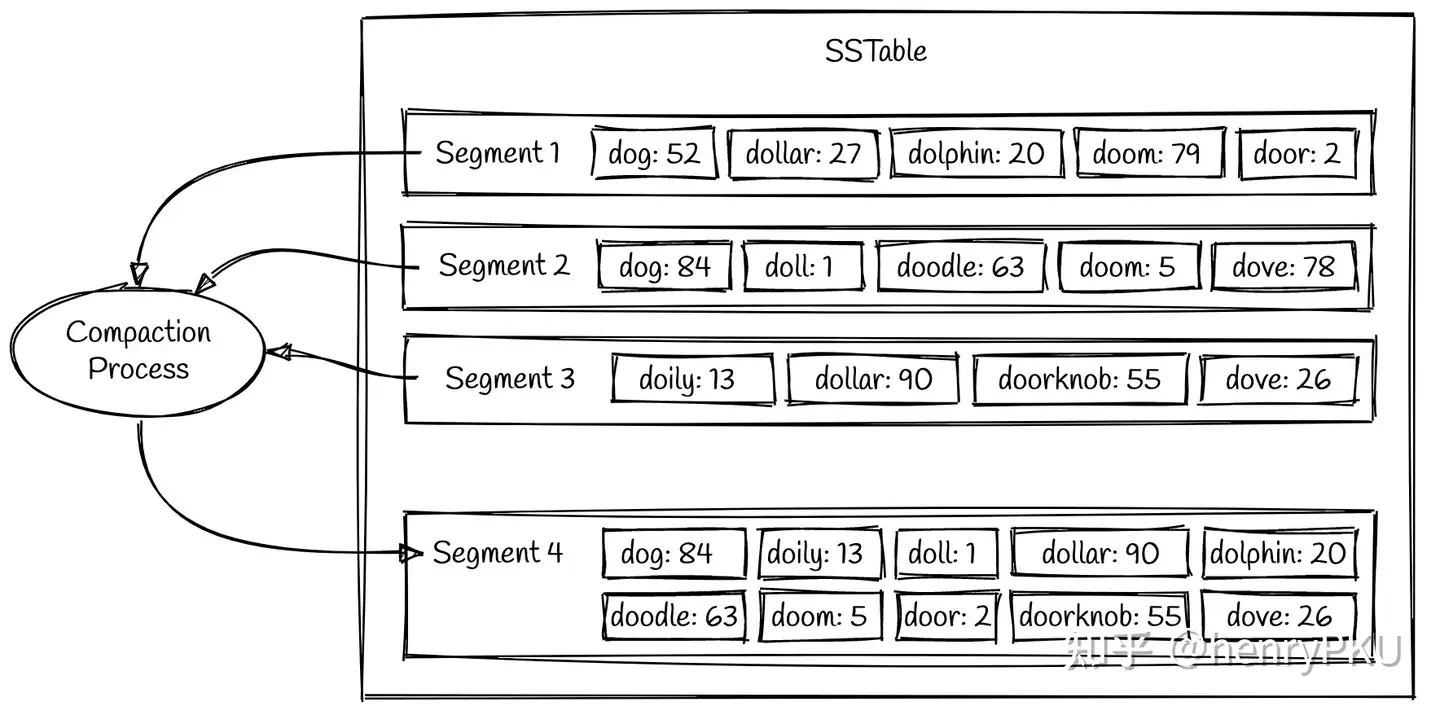
在上图的示例中，segment 1 和 2 中都存在 key 为 dog 的数据，这时应该以最新的 segment 为准，因此合并后的值取 84 而不是 52，这实现了类似于字典/HashMap 中“覆盖写”的语义。

删除数据

总结：删除/更新数据实际为写入新的数据

读取时会按照从新到旧的顺序扫描 segment

合并时相同的Key会以最新的 segment 为准

所以写入相同Key的新数据，即可覆盖旧数据（删除数据写入为墓碑）

要从一个 segment 文件中间抹除一段数据必须要覆写其之后的所有内容，这个成本非常高。

LSM tree 所采用的做法是设计一个特殊的标志位，称为 tombstone（墓碑），删除一条数据就是把它的 value 置为墓碑，如下图所示：

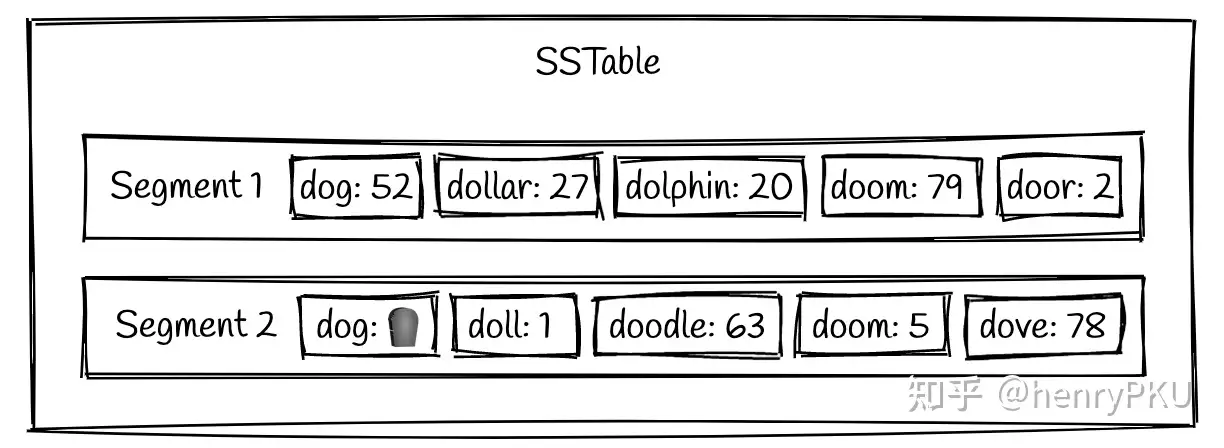
这个例子展示了删除 segment 2 中的 dog 之后的效果。注意，此时 segment 1 中仍然保留着 dog 的旧数据，如果我们查询 dog，那么应该返回空，而不是 52。因此，删除操作的本质是覆盖写，而不是清除一条数据，这一点初看起来不太符合常识。墓碑会在 compact 操作中被清理掉，于是置为墓碑的数据在新的 segment 中将不复存在。

LSM tree 与 B tree 的对比

主流的关系型数据库均以 B/B+ tree 作为其构建索引的数据结构，这是因为 B tree 提供了理论上最高的查询效率 O(log⁡n) 。

但对查询性能的追求也造成了 B tree 的相应缺点，即每次插入或删除一条数据时，均需要更新索引，从而造成一次磁盘 IO。这种特性决定了 B tree 只适用于频繁读、较少写的场景。如果在频繁写的场景下，将造成大量的磁盘 IO，从而导致性能骤降。这种应用场景在传统的关系型数据库中比较常见。

而 LSM tree 则避免了频繁写场景下的磁盘 IO 开销，尽管其查询效率无法达到理想的 O(log⁡n) ，但依然非常快，可以接受。

所以从本质上来说，LSM tree 相当于牺牲了一部分查询性能，换取了可观的写入性能。这对于 key-value 型或日志型数据库是非常重要的。

总结

LSM tree 存储引擎的工作原理包含以下几个要点：

写数据时，首先将数据缓存到内存中的一个有序树结构中（称为 memtable）。同时触发相关结构的更新，例如布隆过滤器、稀疏索引。
当 memtable 积累到足够大时，会一次性写入磁盘中，生成一个内部有序的 segment 文件。该过程为连续写，因此效率极高。
进行查询时，首先检查布隆过滤器。如果布隆过滤器报告数据不存在，则直接返回不存在。否则，按照从新到老的顺序依次查询每个 segment。
在查询每个 segment 时，首先使用二分搜索检索对应的稀疏索引，找到数据所在的 offset 范围。然后读取磁盘上该范围内的数据，再次进行二分查找并获得结果。
对于大量的 segment 文件，定期在后台执行 compaction 操作，将多个文件合并为更大的文件，以保证查询效率不衰减。

深入总结

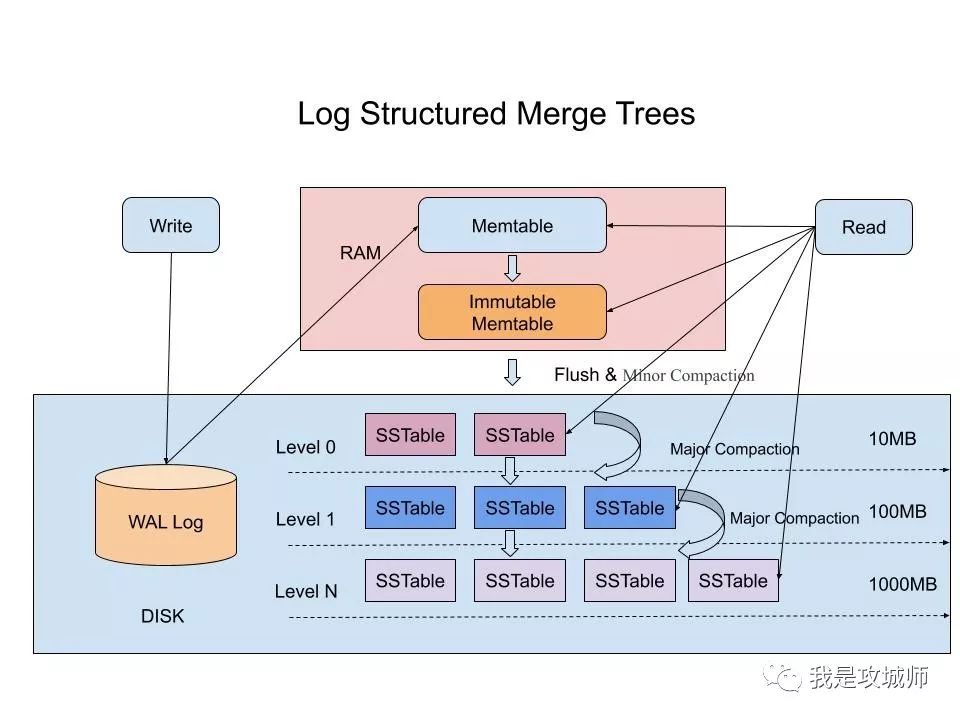
如何写数据

当收到一个写请求时，会先把该条数据记录在 WAL Log 里面，用作故障恢复。
当写完 WAL Log 后，会把该条数据写入内存的 SSTable 里面（删除是墓碑标记，更新是新记录一条的数据），也称 Memtable。注意为了维持有序性在内存里面可以采用红黑树或者跳跃表相关的数据结构。
当 Memtable 超过一定的大小后，会在内存里面冻结，变成不可变的 Memtable，同时为了不阻塞写操作需要新生成一个 Memtable 继续提供服务。
把内存里面不可变的 Memtable 给 dump 到到硬盘上的 SSTable 层中，此步骤也称为 Minor Compaction，这里需要注意在 L0 层的 SSTable 是没有进行合并的，所以这里的key range在多个SSTable中可能会出现重叠，在层数大于0层之后的 SSTable，不存在重叠key。
当每层的磁盘上的 SSTable 的体积超过一定的大小或者个数，也会周期的进行合并。此步骤也称为 Major Compaction，这个阶段会真正的清除掉被标记删除掉的数据以及多版本数据的合并，避免浪费空间，注意由于 SSTable 都是有序的，我们可以直接采用 merge sort 进行高效合并。

如何读数据

当收到一个读请求的时候，会直接先在内存里面查询，如果查询到就返回。
如果没有查询到就会依次下沉，知道把所有的 Level 层查询一遍得到最终结果。

做的改进

思考查询步骤，我们会发现如果 SSTable 的分层越多，那么最坏的情况下要把所有的分层扫描一遍，对于这种情况肯定是需要优化的，如何优化？在 Bigtable 论文中提出了几种方式：

压缩

SSTable 是可以启用压缩功能的，并且这种压缩不是将整个 SSTable 一起压缩，而是根据 locality 将数据分组，每个组分别压缩，这样的好处当读取数据的时候，我们不需要解压缩整个文件而是解压缩部分 Group 就可以读取。

缓存

因为SSTable在写入磁盘后，除了Compaction之外，是不会变化的，所以我可以将Scan的Block进行缓存，从而提高检索的效率

索引，Bloom filters - 布隆过滤器

正常情况下，一个读操作是需要读取所有的 SSTable 将结果合并后返回的，但是对于某些 key 而言，有些 SSTable 是根本不包含对应数据的，因此，我们可以对每一个 SSTable 添加 Bloom Filter，因为布隆过滤器在判断一个SSTable不存在某个key的时候，那么就一定不会存在，利用这个特性可以减少不必要的磁盘扫描。

合并

这个在前面的写入流程中已经介绍过，通过定期合并瘦身，可以有效的清除无效数据，缩短读取路径，提高磁盘利用空间。但Compaction操作是非常消耗CPU和磁盘IO的，尤其是在业务高峰期，如果发生了Major Compaction，则会降低整个系统的吞吐量，这也是一些NoSQL数据库，比如Hbase里面常常会禁用Major Compaction，并在凌晨业务低峰期进行合并的原因。

为什么LSM不直接顺序写入磁盘，而是需要在内存中缓冲一下？

单条写的性能肯定没有批量写来的块，这个原理其实在Kafka里面也是一样的，虽然kafka给我们的感觉是写入后就落地，但其实并不是，本身是可以根据条数或者时间比如200ms刷入磁盘一次，这样能大大提升写入效率。此外在LSM中，在磁盘缓冲的另一个好处是，针对新增的数据，可以直接查询返回，能够避免一定的IO操作。