TBH个人博客
回溯算法总结[更新ing]
tbghg
  2023-03-01 22:54:17   2023-03-01 22:54:17    1.6k 字  6 分钟

Golang写回溯注意事项

!重点! 最需要注意的三个地方

简记：调用回溯函数、path切片复制装入res、for循环区分 idx 和 i

  1. 闭包写完回溯函数后，不要忘记 调用回溯函数
  2. 将path装入result时，不可直接添加需要复制
    【res = append(res, path)，如果path还接着用，那原本装在res的切片也会跟着更改，正确做法：res = append(res, append([]int{}, path...))】
  3. for循环内部调用时，注意dfs里传入start(初始值) 还是i(当前值) 还是 其他【比较容易马虎写串】

复制数组时，可以copy，也可以...拆分后重组

1
2
3
4
5
6
// 方法一：copy
tmp := make([]int,len(path)) // 注意：长度必须和path一致
copy(tmp, path)
res = append(res, tmp)
// 方法二：拆分后重组
res = append(res,append([]int{},path...))

注意copy的用法：不会因为srcSlice大而发生扩容，destSlice分配过多少空间就写多少空间

copy( destSlice, srcSlice []T) int

前言

回溯算法规律性太强了，写个总结以后也方便复习。根据代码随想录总结的，插了些自己的看法

回溯介绍

介绍

回溯法也可以叫做回溯搜索法，它是一种搜索的方式。回溯的本质是穷举，但也可以加一些剪枝的操作

有的问题暴力直接写写不出来，此时需要借助回溯实现暴力，回溯可解决的常见问题有：

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 棋盘问题：N皇后，解数独等

回溯法解决的问题都可以抽象为树形结构

image

1
2
3
4
5
6
7
8
9
10
11
12
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

需要注意力扣中全局变量的用法：力扣全局变量，力扣里面，全局变量只初始化一次，之后只是调用目标函数，所以在函数内部初始化

1
2
3
4
5
6
7
8
9
10
11
var (
	path   []int
	result [][]int
)
// 假设combine为力扣入口函数
func combine(n int, k int) [][]int {
	path = make([]int, 0,k)		// 全局变量必须函数内部再次初始化
	result = make([][]int, 0)
	backtrack(n, k, 1)
	return result
}

我这里推荐直接写闭包，个人喜欢将回溯函数命名dfs

题目分类

组合问题

介绍

77 组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。你可以按 任何顺序 返回答案。

示例 1：

1
2
3
4
5
6
7
8
9
10
输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

示例 2：

1
2
输入：n = 1, k = 1
输出：[[1]]

提示：

  • 1 <= n <= 20
  • 1 <= k <= n

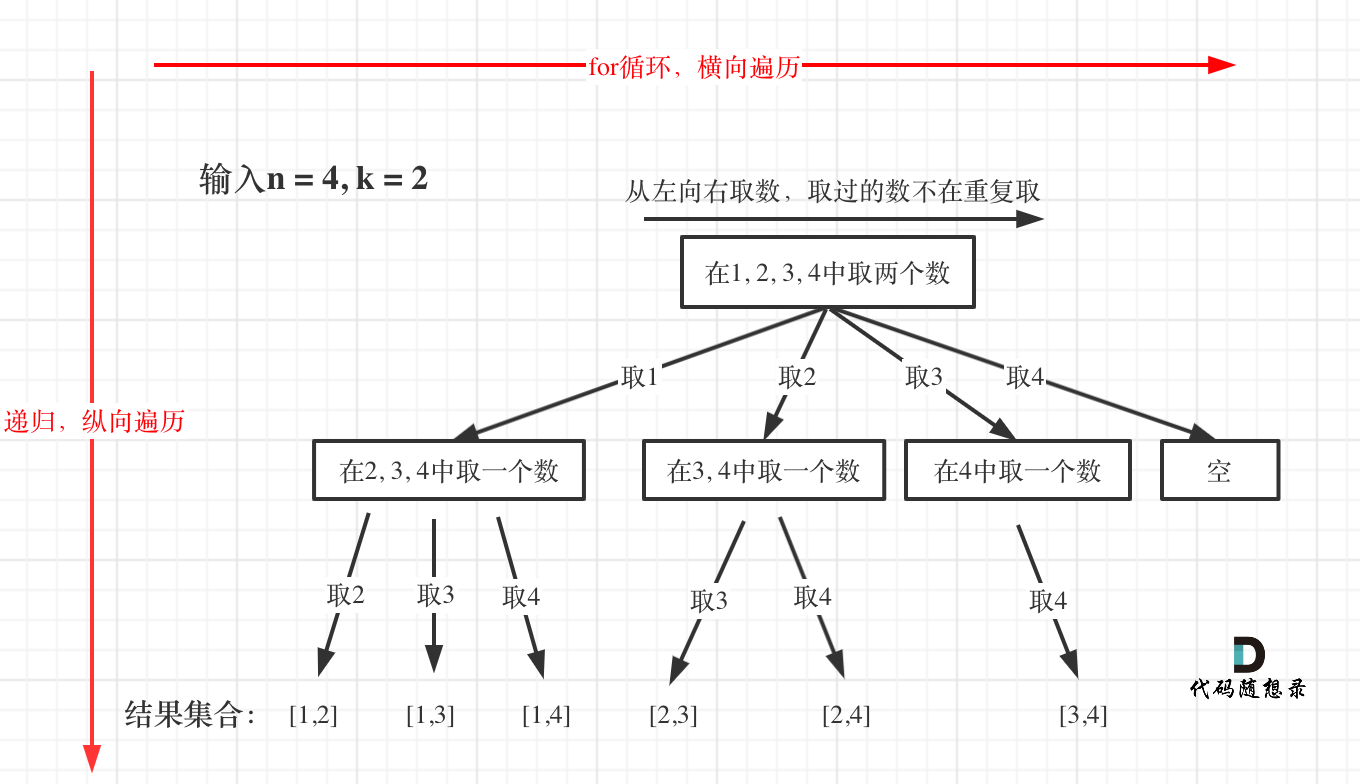
image

重点：左侧取1的那个分支 会包含 所有 取数组中下表为0的情况，所以之后从2、3、4开始取时不用管那个1了，这个是在回溯内部的for循环中实现的，而 树往下延申 是 通过回溯实现

图中可以发现n相当于树的宽度，k相当于树的深度，每次搜索到了叶子节点，我们就找到了一个结果

只需要把达到叶子节点的结果收集起来，就可以求得n个数中k个数的组合集合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
func combine(n int, k int) [][]int {
	path := make([]int, 0, k)
	res := make([][]int, 0)
	// 先声明再赋值，若直接dfs := func(...){...} 无法在内部递归调用
	var dfs func(int)
	dfs = func(idx int) {
		if len(path) == k {
			res = append(res, append([]int{}, path...))
		}
		for i := idx; i <= n; i++ {
			path = append(path, i)
			// 进入包含下标为i的分支
			dfs(i+1)  // 子节点不再重复选自己，所以 i+1
			path = path[:len(path)-1]
		}
	}
	dfs(1)  // 记着调用
	return res
}

注意，回溯的题都要考虑是否可以 剪枝优化

这道题，当 还剩的节点数目 + path中已经选中的 < k ，即 n-i+1 + len(path) < k该节点及其子节点肯定都不满足，没必要接着for循环了，直接return

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
func combine(n int, k int) [][]int {
	path := make([]int, 0, k)
	res := make([][]int, 0)
	var dfs func(int)
	dfs = func(idx int) {
		if len(path) == k {
			res = append(res, append([]int{}, path...))
		}
		for i := idx; i <= n; i++ {
			// 剩下?数可选 < 总共还要选?个数
			// 也可移项后写入for判断条件中
            if n - i + 1 < k - len(path) { // 剪枝
                return
	        }
			path = append(path, i)
			// 进入包含下标为i的分支
			dfs(i+1)  // 子节点不再重复选自己，所以 i+1
			path = path[:len(path)-1]
		}
	}
	dfs(1)  // 记着调用
	return res
}

216 组合总和 III

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

  • 只使用数字1到9
  • 每个数字 最多使用一次

返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

1
2
3
4
5
输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

1
2
3
4
5
6
7
输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

1
2
3
4
输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示:

  • 2 <= k <= 9
  • 1 <= n <= 60

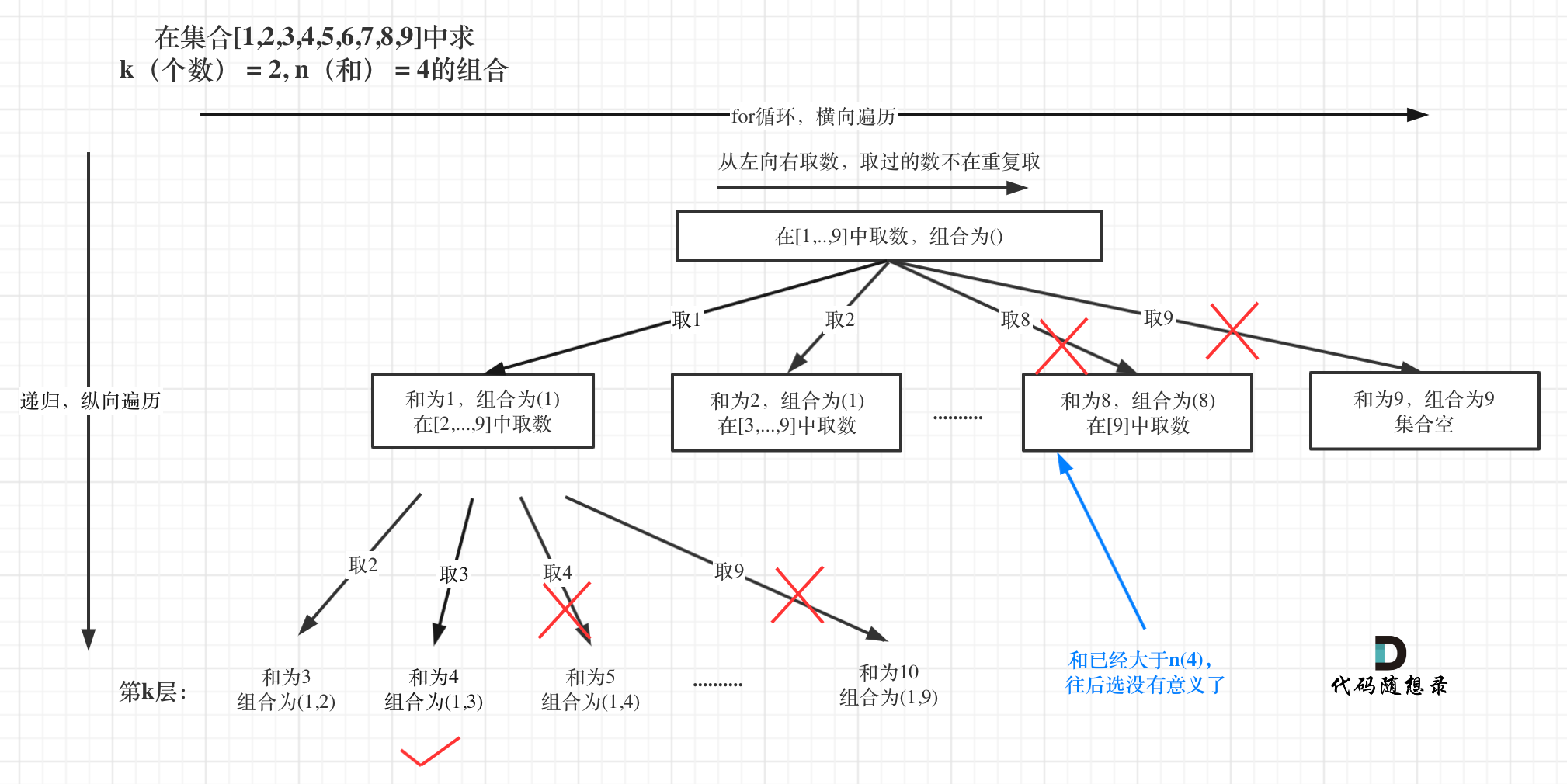
k 相当于树的深度，9（因为整个集合就是9个数）就是树的宽度

例如 k = 2，n = 4 的话，就是在集合[1,2,3,4,5,6,7,8,9]中求 k（个数） = 2, n（和） = 4的组合。

image

 评论
评论插件加载失败
正在加载评论插件
  1. 1. Golang写回溯注意事项
  2. 2. 前言
  3. 3. 回溯介绍
    1. 3.1. 介绍
    2. 3.2. 题目分类
  4. 4. 组合问题
    1. 4.1. 介绍
    2. 4.2. 77 组合
    3. 4.3. 216 组合总和 III
  1. 1. Golang写回溯注意事项
  2. 2. 前言
  3. 3. 回溯介绍
    1. 3.1. 介绍
    2. 3.2. 题目分类
  4. 4. 组合问题
    1. 4.1. 介绍
    2. 4.2. 77 组合
    3. 4.3. 216 组合总和 III