前言
最近复习了下排序算法,常用的都用go敲了一遍。练习排序可以在牛客的这道试题中进行测试。
菜鸟教程关于排序这块介绍的挺详细的,还配有动图,比较推荐。另外B站上马士兵老师在计数排序、基数排序这块进行了拓展,感觉说的也很棒
简要总结
![image]()
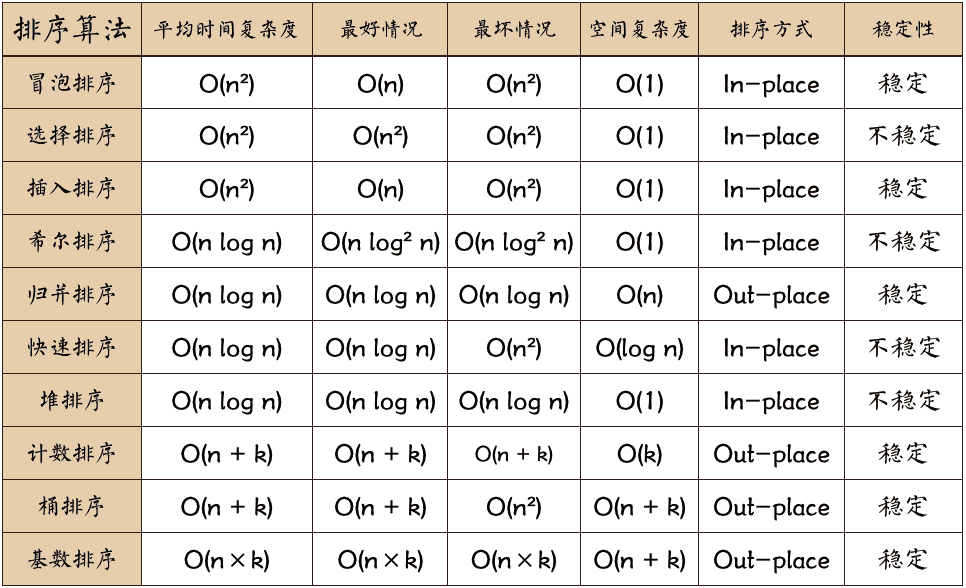
排序算法总结
- 快速排序和归并排序都使用了分治和递归
- 从时间性能上看,快速排序是所有排序算法中实际性能最好的,然而快速排序在最坏情况下(数据基本有序)的时间性能不如堆排序和归并排序,并且空间复杂度高,所以更适合数据不大的情况
- 堆排序在任何情况下,其时间复杂度为 Ο(nlogn)。这相对于快速排序而言是堆排序的最大优点。堆排序在元素较少时由于消耗较多时间在初始建堆上,因此不值得提倡,然而当元素较多时还是很有效的排序算法
- 与快速排序和堆排序相比,归并排序的优点是它是一种稳定的排序方法,最坏情况下时间性能好
- 从方法稳定性上来看,大多数时间复杂度为Ο(n^2)的排序均是稳定的排序方法,除简单选择排序之外。而多数时间性能较好的排序方法,例如快速排序、堆排序、希尔排序都是不稳定的
- 基于比较的排序的时间复杂度下限是O(nlogn),即这已经是最高的效率了
基数排序和计数排序是非比较的排序的排序,都是桶思想,可以达到线性时间O(n)复杂度的排序,但是使用范围不太广。其中计数排序如果直接计数然后按照数量输出相应次数是不具有稳定性的,但是可以通过累加数组(前缀和)的形式先加一遍,然后逆序遍历原数组输出,即可保证稳定性。
计数排序场景示例:300W考生排名
冒泡排序
依次比较相邻的两个元素,按照升序或者降序的规则进行交换
稳定、平均时间O(n^2)、最好时间O(n)、最差时间O(n^2)、空间复杂度O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
func bubbleSort(length int, source []int) []int {
for i := 0; i < length; i++ {
isSort := true
for j := 0; j < length-i-1; j++ {
if source[j] > source[j+1] {
source[j], source[j+1] = source[j+1], source[j]
isSort = false
}
}
if isSort {
break
}
}
return source
}
|
选择排序
平均时间O(n^2)、最好时间O(n^2)、最坏时间O(n^2)、不稳定、空间复杂度O(1)
从待排序的数据元素中选出最小(或最大)的一个元素,存放在待排序序列起始位置,直到全部待排序的数据元素的个数为零
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
func selectSort(length int, source []int) []int {
for i := 0; i < length-1; i++ {
minIdx, maxMin := i, source[i]
for j := i + 1; j < length; j++ {
if source[j] < maxMin {
minIdx = j
maxMin = source[j]
}
}
if minIdx != i {
source[minIdx], source[i] = source[i], source[minIdx]
}
}
return source
}
|
插入排序
将一个数据插入到已经排好序的有序数据中,从而得到一个新的、个数加一的有序数据
平均时间O(n^2)、最好时间O(n)、最差时间O(n^2)、稳定、空间复杂度O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
func insertSort(length int, source []int) []int {
for i := 1; i < length; i++ {
insertVal := source[i]
insertIdx := i
for insertIdx > 0 && source[insertIdx-1] > insertVal {
source[insertIdx] = source[insertIdx-1]
insertIdx--
}
if insertIdx != i {
source[insertIdx] = insertVal
}
}
return source
}
|
希尔排序
简要概括
按照下标一定增量进行分组,每组再按照直接插入算法排序,随着组的减少,每组的元素也越来越少,当组数减少至为1时,整个文件分成1组,算法便终止。
希尔排序写的时候最好先把直接插入排序想一遍,要不循环那里容易晕
平均时间O(n^1.3~n^2)、最好时间O(n)、最坏时间O(n^2)、不稳定、空间复杂度O(1)
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
func shellSort(length int, source []int) []int {
for gap := length / 2; gap > 0; gap /= 2 {
for i := 0; i < gap; i++ {
for j := i + gap; j < length; j += gap {
insertIdx := j
insertVal := source[j]
for insertIdx > i && source[insertIdx-gap] > insertVal {
source[insertIdx] = source[insertIdx-gap]
insertIdx -= gap
}
if insertIdx != j {
source[insertIdx] = insertVal
}
}
}
}
return source
}
|
快速排序
简要概括
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。大致意思就是在一个数组中取中间元素比它小的方左边比它大的则放右边两边元素再按照快排要求,最终变成有序序列。
平均时间O(nlogn)、最好时间O(nlogn)、最坏时间O(n^2)、不稳定、空间复杂度O(nlogn)
注意:当序列为为正序或逆序排列时为最坏时间,此时时间复杂度O(n^2)
快排实现思路
快速排序通过递归实现,一般是俩函数:
- quickSort递归函数:
- 快排的入口并调用递归
- 终止条件: l >= r
- 参数: 切片 l r
- 返回值: 无
- partition定位pivot函数
- 交换
- 返回pivot最后的位置
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| func quickSort(source []int, l int, r int) {
if l >= r {
return
}
q := partition(source, l, r)
quickSort(source, l, q-1)
quickSort(source, q+1, r)
}
func partition(nums []int, l int, r int) int {
end, pivot := r, nums[r]
for l < r {
for l < r && nums[l] <= pivot {
l++
}
for l < r && nums[r] >= pivot {
r--
}
nums[l], nums[r] = nums[r], nums[l]
}
nums[l], nums[end] = pivot, nums[l]
return l
}
|
堆排序
简要概括
堆排序这个视频讲的不错,但是这个人讲的计数排序有较大问题
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法:
- 大顶堆:每个节点的值都大于或等于其子节点的值,在堆排序算法中用于升序排列
- 小顶堆:每个节点的值都小于或等于其子节点的值,在堆排序算法中用于降序排列
平均时间O(nlogn)、最好时间O(nlogn)、最差时间O(nlogn)、不稳定、空间复杂度O(1)
重点
堆排序中最中要的式子:
- 下标为 i 的节点的父节点下标:( i - 1) / 2
- 下标为 i 的节点的左孩子下标:i * 2 + 1
- 下标为 i 的节点的右孩子下标:i * 2 + 2
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
func keepHeap(source []int, n int, change int) {
lSon := change*2 + 1
rSon := change*2 + 2
maxIdx := change
if lSon < n && source[lSon] > source[maxIdx] {
maxIdx = lSon
}
if rSon < n && source[rSon] > source[maxIdx] {
maxIdx = rSon
}
if maxIdx != change {
source[maxIdx], source[change] = source[change], source[maxIdx]
keepHeap(source, n, maxIdx)
}
}
func heapSort(source []int, length int) {
for i := length/2 - 1; i >= 0; i-- {
keepHeap(source, length, i)
}
for i := length - 1; i >= 0; i-- {
source[0], source[i] = source[i], source[0]
keepHeap(source, i, 0)
}
}
|
归并排序
简要概括
建立在归并操作上的一种有效的排序算法。该算法是采用分治法的一个非常典型的应用
将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
平均时间O(nlogn)、最好时间O(nlogn)、最坏时间O(nlogn)、稳定、空间复杂度O(n)
代码实现
go这块因为操作的切片底层数组时一样的,所以没必要用left、right标记头尾,直接切割就行,反正会复用底层数组,不会浪费空间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
|
func mergeSort(arr []int) []int {
length := len(arr)
if length < 2 {
return arr
}
middle := length / 2
left := arr[0:middle]
right := arr[middle:]
return merge(mergeSort(left), mergeSort(right))
}
func merge(left []int, right []int) []int {
var result []int
for len(left) != 0 && len(right) != 0 {
if left[0] <= right[0] {
result = append(result, left[0])
left = left[1:]
} else {
result = append(result, right[0])
right = right[1:]
}
}
for len(left) != 0 {
result = append(result, left[0])
left = left[1:]
}
for len(right) != 0 {
result = append(result, right[0])
right = right[1:]
}
return result
}
|
参考文章