算法总结——队列

0. 理论基础

队列queue

在计算机科学中，一个队列queue 是一种特殊的抽象数据类型(Abstract Data Type) 或其中元素保持一定顺序的集合。其中最主要的（或则说唯一的）的在此集合上的操作是加元素到队列的末端，被称为入队/入列 enqueue；将元素从队列的前段移除，则称为出队/出列 dequeue；这让队列成为了先进先出（First-In-First-Out，FIFO）的数据结构。在先进先出的数据结构中，添加到队列中的第一个元素将会是第一个被删除的元素。队列是线性数据结构中的一种，或者更抽象地说，是一种顺序收集sequential collection。

双端队列 Double-ended queue

双端队列 Double-ended queue，简称为Deque，和队列的操作方式出列同名但不是一个意思。 在计算机科学中，双端队列(缩写为deque) 是一种抽象数据类型，它概括了一个队列，其中的元素可以从前(头) 或后(尾) 添加或删除。因此也经常被称为首尾链表。

主要操作

• InitQueue(&Q)：初始化队列，构造一个空队列Q。
• QueueEmpty(Q)：判队列空，若队列Q为空返回true，否则返回false。
• EnQueue(&Q, x)：入队，若队列Q未满，将x加入，使之成为新的队尾。
• DeQueue(&Q, &x)：出队，若队列Q非空，删除队头元素，并用x返回。
• GetHead(Q, &x)：读队头元素，若队列Q非空，则将队头元素赋值给X。

实现

1. 顺序存储结构—-基于数组
2. 链式存储结构—-基于单链表

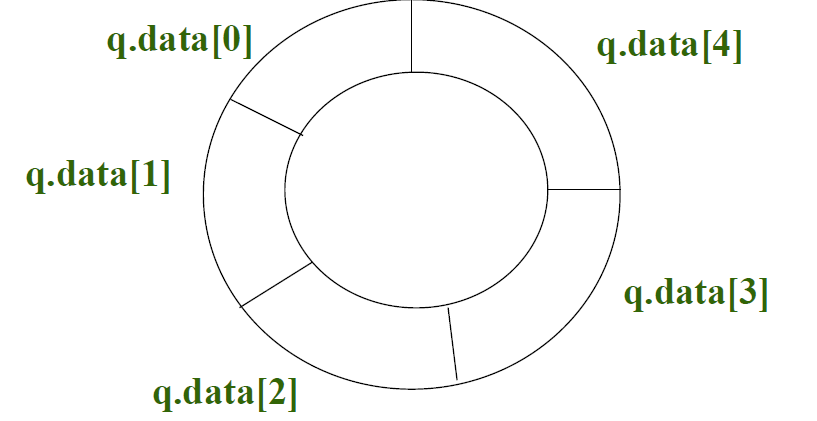
顺序存储结构

队列的主要操作在队首和队尾处完成 ，要保留队头、队尾两个位置方便操作实现

#define MAXSIZE 5
typedef struct
{
    elemtype data[MAXSIZE];
    int f, r; //队首和队尾指针
} SeQueue;
SeQueue q;

说明：elemtype代表队列中数据元素的类型，具体应用时，队列中的数据元素是什么类型的，就将elemtype定义成相应类型

基本操作：

// 初始化
q.f=0;q.r=0;
// 入队
if (q.r < MAXSIZE) { // 判断是否溢出
    q.data[q.r]=x;
    q.r++;
} else printf(“overflow”);
// 出队
if ( q.f != q.r ) q.f++;

思考一个问题，随着不断入队出队，q.f、q.r一直在增长，最后q.r = MAXSIZE时，即使队列只有或者为空均会因为没有空间而无法再插入——顺序队列存在假溢出。

解决方式：

1. 每删除一个数据元素，余下的所有数据元素顺次移动一个位置——效率太低
2. 循环队列，首尾相接

循环队列

将正常的数组空间看成环状的，通过求余（%，MOD）运算可实现数组的首尾相接

判断队满

队空和队满时q.f==q.r，无法根据队首和队尾指针的相对位置判断队列是处于“空”还是处于“满”的状态

• 方法1：设一计数器，初始化时计数器清0，入队时，计数器+1，出队时计数器-1
• 方法2：为区分队空、队满，牺牲一个存储位置，当(q.r+1)%MAXSIZE==q.f时认为队满了，q.r==q.f为队空

基本操作

// 初始化
q.f=0;q.r=0;
// 入队
if( (q.r+1)%MAXSIZE==q.f ) { // 此处为方法2，判断是否溢出
    q.data[q.r]=x;
    q.r=(q.r+1)%MAXSIZE;
} else printf(“overflow”);
// 出队
if( q.r==q.f ) q.f = (q.f+1)%MAXSIZE;

链式存储结构

f为队首指针，指示链队的队首位置
r为队尾指针，指示链队的队尾位置

比较基础，学完链表之后这个挺轻松的，不多解释

// 入队
s=(LinkList)malloc(sizeof(Node));
s->data=x;
r->next=s;
s->next=NULL;
r=s;
// 出队
s=f->next;
f->next=s->next;
free(s);

1.循环队列

题目链接

请不要使用内置的队列库。

设计你的循环队列实现。 循环队列是一种线性数据结构，其操作表现基于 FIFO（先进先出）原则并且队尾被连接在队首之后以形成一个循环。它也被称为“环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

• MyCircularQueue(k): 构造器，设置队列长度为 k 。
• Front: 从队首获取元素。如果队列为空，返回 -1 。
• Rear: 获取队尾元素。如果队列为空，返回 -1 。
• enQueue(value): 向循环队列插入一个元素。如果成功插入则返回真。
• deQueue(): 从循环队列中删除一个元素。如果成功删除则返回真。
• isEmpty(): 检查循环队列是否为空。
• isFull(): 检查循环队列是否已满。

其中：

• 所有的值都在 0 至 1000 的范围内；
• 操作数将在 1 至 1000 的范围内；

答案

注意事项：

1. 在C语言中负数求余：被除数的绝对值与除数绝对值取余的值即为余数绝对值，余数符号与被除数一致。
2. C语言中使用bool可以#include<stdbool.h>

typedef struct {
    int MAXSIZE;
    int *data;
    int f, r;
} MyCircularQueue;

MyCircularQueue *myCircularQueueCreate(int k) {
    MyCircularQueue *CQ = (MyCircularQueue *) malloc(sizeof(MyCircularQueue));
    CQ->r = 0, CQ->f = 0;
    CQ->MAXSIZE = k + 1; // 牺牲一个存储位置，判断队满
    CQ->data = (int *) malloc(sizeof(int *) * CQ->MAXSIZE);
    return CQ;
}

bool myCircularQueueEnQueue(MyCircularQueue *obj, int value) {
    if ((obj->r + 1) % obj->MAXSIZE != obj->f) {
        obj->data[obj->r] = value;
        obj->r = (obj->r + 1) % obj->MAXSIZE;
        return true;
    } else return false;
}

bool myCircularQueueDeQueue(MyCircularQueue *obj) {
    if (obj->f != obj->r) {
        obj->f = (obj->f + 1) % obj->MAXSIZE;
        return true;
    } else return false;
}

int myCircularQueueFront(MyCircularQueue *obj) {
    if (obj->f != obj->r) return obj->data[obj->f];
    else return -1;
}

int myCircularQueueRear(MyCircularQueue *obj) {
    if (obj->f != obj->r) return obj->data[(obj->r - 1 + obj->MAXSIZE) % obj->MAXSIZE];
    else return -1;
}

bool myCircularQueueIsEmpty(MyCircularQueue *obj) {
    return obj->f == obj->r;
}

bool myCircularQueueIsFull(MyCircularQueue *obj) {
    return (obj->r + 1) % obj->MAXSIZE == obj->f;
}

void myCircularQueueFree(MyCircularQueue *obj) {
    free(obj->data);
    free(obj);
}

2. 循环双端队列

题目链接

设计实现双端队列。

实现 MyCircularDeque 类:

• MyCircularDeque(int k) ：构造函数,双端队列最大为 k 。
• boolean insertFront()：将一个元素添加到双端队列头部。 如果操作成功返回 true ，否则返回 false 。
• boolean insertLast() ：将一个元素添加到双端队列尾部。如果操作成功返回 true ，否则返回 false 。
• boolean deleteFront() ：从双端队列头部删除一个元素。 如果操作成功返回 true ，否则返回 false 。
• boolean deleteLast() ：从双端队列尾部删除一个元素。如果操作成功返回 true ，否则返回 false 。
• int getFront() )：从双端队列头部获得一个元素。如果双端队列为空，返回 -1 。
• int getRear() ：获得双端队列的最后一个元素。 如果双端队列为空，返回 -1 。
• boolean isEmpty() ：若双端队列为空，则返回 true ，否则返回 false 。
• boolean isFull() ：若双端队列满了，则返回 true ，否则返回 false 。

示例 1：

输入
["MyCircularDeque", "insertLast", "insertLast", "insertFront", "insertFront", "getRear", "isFull", "deleteLast", "insertFront", "getFront"]
[[3], [1], [2], [3], [4], [], [], [], [4], []]
输出
[null, true, true, true, false, 2, true, true, true, 4]

其中：

• 1 <= k <= 1000
• 0 <= value <= 1000
• insertFront, insertLast, deleteFront, deleteLast, getFront, getRear, isEmpty, isFull 调用次数不大于 2000 次

代码

注意实现与循环队列相同，只需要在循环队列的基础上加上队头删除、队尾插入，其余保持不变，没啥难度，不多介绍

typedef struct {
    int MAXSIZE;
    int *data;
    int f, r;
} MyCircularDeque;

MyCircularDeque *myCircularDequeCreate(int k) {
    MyCircularDeque *CD = (MyCircularDeque *) malloc(sizeof(MyCircularDeque));
    CD->r = 0, CD->f = 0;
    CD->MAXSIZE = k + 1; // 牺牲一个存储位置，判断队满
    CD->data = (int *) malloc(sizeof(int *) * CD->MAXSIZE);
    return CD;
}

bool myCircularDequeInsertFront(MyCircularDeque *obj, int value) {
    if ((obj->r + 1) % obj->MAXSIZE != obj->f) {
        obj->f = (obj->f - 1 + obj->MAXSIZE) % obj->MAXSIZE; // 头指针向前走一位，然后插入数据
        obj->data[obj->f] = value;
        return true;
    } else return false;
}

bool myCircularDequeInsertLast(MyCircularDeque *obj, int value) {
    if ((obj->r + 1) % obj->MAXSIZE != obj->f) {
        obj->data[obj->r] = value;
        obj->r = (obj->r + 1) % obj->MAXSIZE;
        return true;
    } else return false;
}

bool myCircularDequeDeleteFront(MyCircularDeque *obj) {
    if (obj->f != obj->r) {
        obj->f = (obj->f + 1) % obj->MAXSIZE;
        return true;
    } else return false;
}

bool myCircularDequeDeleteLast(MyCircularDeque *obj) {
    if (obj->f != obj->r) {
        obj->r = (obj->r - 1 + obj->MAXSIZE) % obj->MAXSIZE;
        return true;
    } else return false;
}

int myCircularDequeGetFront(MyCircularDeque *obj) {
    if (obj->f != obj->r) return obj->data[obj->f];
    else return -1;
}

int myCircularDequeGetRear(MyCircularDeque *obj) {
    if (obj->f != obj->r) return obj->data[(obj->r - 1 + obj->MAXSIZE) % obj->MAXSIZE];
    else return -1;
}

bool myCircularDequeIsEmpty(MyCircularDeque *obj) {
    return obj->f == obj->r;
}

bool myCircularDequeIsFull(MyCircularDeque *obj) {
    return (obj->r + 1) % obj->MAXSIZE == obj->f;
}

void myCircularDequeFree(MyCircularDeque *obj) {
    free(obj->data);
    free(obj);
}

3. 单调队列

单调队列，顾名思义，是一种具有单调性的队列。众所周知，单调性有单调递增和单调递减两种，相应的单调队列也分为单调递增队列和单调递减队列两种。

• 单调递增队列：保证队列头元素一定是当前队列的最小值，用于维护区间的最小值。
• 单调递减队列：保证队列头元素一定是当前队列的最大值，用于维护区间的最大值。

单独解释起来比较抽象，下面我们通过例题进行讲解

例题一 滑动窗口最大值

题目链接

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值

要求：在线性时间复杂度内解决此题

示例 1：
输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值

[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

示例 2：
输入：nums = [1], k = 1
输出：[1]

说明：

• 1 <= nums.length <= 10^5
• -10^4 <= nums[i] <= 10^4
• 1 <= k <= nums.length

分析

在说具体怎么实现一个单调队列之前，先来一个简单的例子，感受一下：

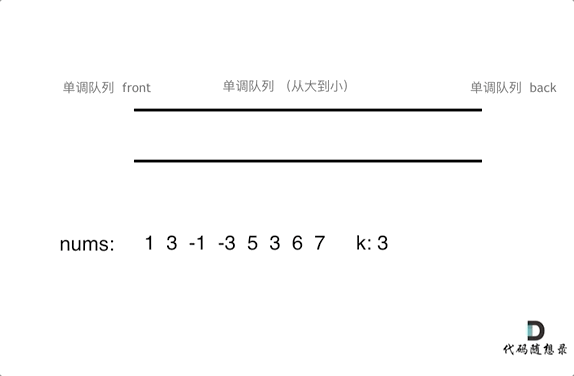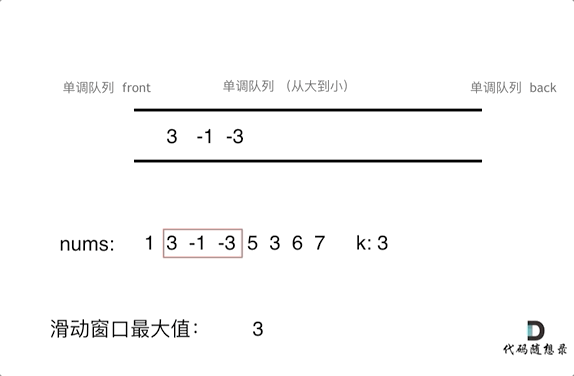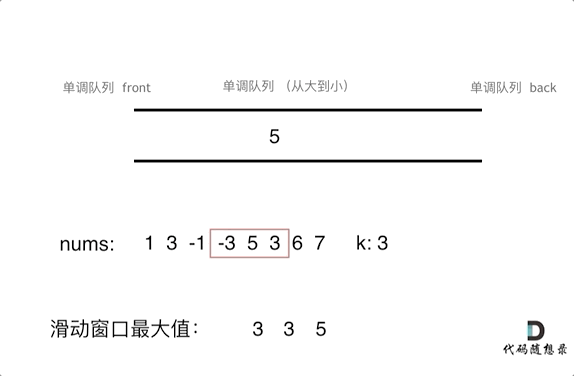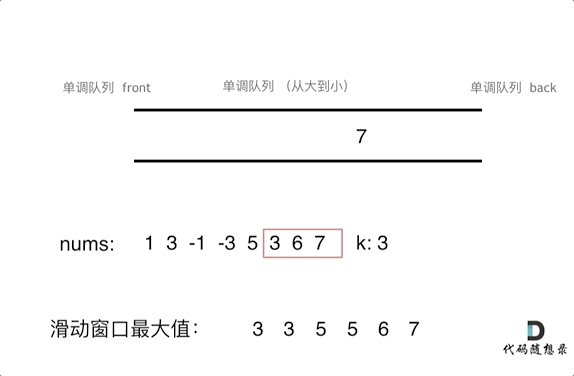
假设给定数列：[ 1, 3, -1, -3, 5, 3, 6, 7 ]，区间长度为3。

用单调队列实现时动画如下：

注意：一般的队列只能从队尾入队、队首出队，为了保持单调队列的单调性，单调队列除具有这两种性质外，还可以从队尾出队。

实现单调队列，主要分为三个部分：

• 去尾操作：队尾元素出队列。当队列有新元素待入队，需要从队尾开始，删除影响队列单调性的元素，维护队列的单调性。(删除一个队尾元素后，就重新判断新的队尾元素)。去尾操作结束后，将该新元素入队列。
• 删头操作：队头元素出队列。判断队头元素是否在待求解的区间之内，如果不在，就将其删除。（这个很好理解呀，因为单调队列的队头元素就是待求解区间的极值）
• 取解操作：经过上面两个操作，取出 队列的头元素，就是当前区间的极值。

关于细节方面的操作可见给出的代码注释

代码

int *maxSlidingWindow(int *nums, int numsSize, int k, int *returnSize)
{
    int q[numsSize];
    int hh = 0, tt = 0; // hh表示队头，tt表示队尾
    // 先将第一个窗口装填完毕
    for (int i = 0; i < k; ++i)
    {
        // hh < tt --> 队列中有数据  q[tt - 1] --> 队尾的数据
        // 如果队列中存在数据且队尾数据比当前数据小，弹出队尾，直到为空或大于等于当前数据
        while (hh < tt && nums[i] >= nums[q[tt - 1]])
        {
            tt--;
        }
        // 将当前数据的下标入队
        q[tt++] = i;
    }

    *returnSize = 0;
    int *ans = (int *)malloc(sizeof(int) * (numsSize - k + 1));
    ans[(*returnSize)++] = nums[q[hh]]; // 将第一个窗口结果写入ans中

    for (int i = k; i < numsSize; ++i)
    {
        // 同上，不做解释
        while (hh < tt && nums[i] >= nums[q[tt - 1]])
        {
            tt--;
        }
        q[tt++] = i;
        // 判断是否超出窗口大小，如果超出队首出队
        while (q[hh] <= i - k)
        {
            hh++;
        }
        // 队首为窗口最大数，写入ans中
        ans[(*returnSize)++] = nums[q[hh]];
    }
    return ans;
}

课后作业

作业一

题目链接

有一个长为 n 的序列 a ，以及一个大小为 k 的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

以下是一个例子：

该数组为 [1 3 -1 -3 5 3 6 7]，k 为 3。

窗口位置

最小值

最大值

[1 3 -1] -3 5 3 6 7

-1

3

1 [3 -1 -3] 5 3 6 7

-3

3

1 3 [-1 -3 5] 3 6 7

-3

5

1 3 -1 [-3 5 3] 6 7

-3

5

1 3 -1 -3 [5 3 6] 7

3

6

1 3 -1 -3 5 [3 6 7]

3

7

你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式：输入一共有两行，第一行有两个正整数 n, k。 第二行 n 个整数，表示序列 a

输出格式：输出包含两个。第一行输出，从左至右，每个位置滑动窗口中的最小值。第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：

8 3
1 3 -1 -3 5 3 6 7

输出样例：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明

题和例题一样，写法和力扣上面的不太一样，就是让大家自己重新写一遍，练一下单调队列。

答案

#include<stdio.h>
#include<malloc.h>

int main() {
    int numsSize, k;
    scanf("%d", &numsSize);
    scanf("%d", &k);
    int *nums = (int *) malloc(sizeof(int) * numsSize); // nums接收数组
    int q[numsSize - k + 1]; // 单调队列存放于q中，存放数据的下标
    int hh = 0, tt = 0; // hh表示队头，tt表示队尾
    for (int i = 0; i < numsSize; i++) {
        scanf("%d", &nums[i]);
        if (i - k + 1 > q[hh]) // 如果队首出窗口，hh++
            hh++;
        while (hh < tt && nums[i] <= nums[q[tt - 1]]) // 若队尾不单增，队尾出队
            tt--;
        q[tt++] = i;
        if (i >= k - 1) // 输出最小值结果
            printf("%d ", nums[q[hh]]);
    }
    printf("\n");
    hh = 0, tt = 0;
    for (int i = 0; i < numsSize; i++) {
        scanf("%d", &nums[i]);
        if (i - k + 1 > q[hh]) // 如果队首出窗口，hh++
            hh++;
        while (hh < tt && nums[i] >= nums[q[tt - 1]]) // 若队尾不单减，队尾出队
            tt--;
        q[tt++] = i;
        if (i >= k - 1) // 输出最大值结果
            printf("%d ", nums[q[hh]]);
    }
    return 0;
}

作业二

题目链接

题目描述

Uim 在公司里面当秘书，现在有 n 条消息要告知老板。每条消息有一个好坏度，这会影响老板的心情。告知完一条消息后，老板的心情等于老板之前的心情加上这条消息的好坏度。最开始老板的心情是 0，一旦老板心情到了 0 以下就会勃然大怒，炒了 Uim 的鱿鱼。

Uim 为了不被炒，提前知道了这些消息（已经按时间的发生顺序进行了排列）的好坏度，希望知道如何才能不让老板发怒。

Uim 必须按照事件的发生顺序逐条将消息告知给老板。不过 Uim 可以使用一种叫 “倒叙” 的手法，例如有 n 条消息，Uim 可以按 k,k+1,k+2,……,n,1,2,……,k-1（事件编号）这种顺序通报。

他希望知道，有多少个 k，可以使从 k 号事件开始通报到 n 号事件然后再从 1 号事件通报到 k-1 号事件可以让老板不发怒。

输入格式

第一行一个整数 n（1 <= n <=10^6），表示有 n 个消息。

第二行 n 个整数，按时间顺序给出第 i 条消息的好坏度 Ai（-10^3<= Ai <= 10^3）。

输出格式

一行一个整数，表示可行的方案个数。

样例

样例输入

4
-3 5 1 2

样例输出

2

【样例解释】
通报事件的可行顺序（用编号表示）为 2–>3–>4–>1 或 3–>4–>1–>2（分别对应 k=2 和 k=3）
通报事件的可行顺序（用好坏度表示）为 5–>1–>2–>(-3) 或 1–>2–>(-3)–>5

【数据范围】
对于 25% 的数据，n<=10^3；
对于 75% 的数据，n<=10^4；
对于 100% 的数据，1 <= n<= 10^6。

答案

首先我们先介入一种思想——断环为链，这样可以方便处理对于每一个k的情况。具体做法可以是将数组双倍展开，说通俗点就是在n后面再接上1到n-1的值

以样例为例：-3 5 1 2，我们将其断环为链后可以得到这样的一组数据：-3 5 1 2 -3 5 1，并设其下标为1–7。当k=1时，需要判断的就是下标1–4；当k=2时，就是下标2–5；当k=3时，就是下标3–6；当k=4时，就是下标4–7（显然k不会等于5）。

断环为链后，题目要求就变为了：对于每一个合法的k，都要满足k–(n+k-1)中，到任意一点的和都是非负的。根据我们之前学到的前缀和，我们可以通过sum[i]表示1–i的所有数的和，那么sum[j]-sum[i-1]就是i–j所有数的和。所以用前缀和预处理后，sum[i]-sum[k-1]就是k–i(k<=i<=n+k-1)的和了，我们只要判断这个和是否为负即可。

既然这么说，那么是否要判断k–n+k-1中每一个数的和呢？当然不是，对比例题一，现在相当于在长度为2n的数组中有一个长度为n的滑动窗口，只需要维护一个单调递增序列，判断每个窗口中最小的sum-sum[k-1]是否为负即可

那么这题的思路就很明确了，先对输入数据断环为链，然后在链上进行前缀和的预处理，最后，对于每一个k+n-1，我们用单调队列维护k–k+n-1的sum最小值，并将其减去sum[k-1]判断是否合法。

#include<stdio.h>
#include<malloc.h>

int main() {
    int n, head = 0, tail = 0, ans = 0;
    scanf("%d", &n);
    long *a = (long *) malloc(sizeof(long) * n);
    long *q = (long *) malloc(sizeof(long) * n);
    long *sum = (long *) malloc(sizeof(long) * n * 2);

    for (int i = 0; i < n; i++)
        scanf("%ld", &a[i]);
    // 计算前缀和
    for (int i = 0; i < n; i++)
        sum[i] = sum[i - 1] + a[i];
    for (int i = n; i < 2 * n; i++)
        sum[i] = sum[i - 1] + a[i - n];
    // 维护单调队列
    for (int i = 0; i < 2 * n; i++) {
        if (i - n + 1 > q[head])head++;
        while (head < tail && sum[i] <= sum[q[tail - 1]])tail--;
        q[tail++] = i;
        if (i - n + 1 > 0 && sum[q[head]] - sum[i - n] >= 0)ans++;
    }
    printf("%d\n", ans);
    return 0;
}

4. 优先队列

普通的队列具有先进先出的特性，元素追加在队尾，如果删除的话，从队头删除。而在优先队列中，队列中的数据被赋予了优先级。当访问元素时，优先级最高的会先被删除。所以说优先队列是最高级数据先出。

优先队列的操作：

1. 删除最小（最大）元素
2. 插入一个元素

优先队列需要维护一个有序的元素序列，但不要求全部有序，只需要从这些元素中找到最大（或最小）的一个元素，而堆正好满足这一要求。关于堆，我们会在排序模块进行详细介绍，下面我会简单的介绍一下。

堆就是用数组实现的二叉树，分为大顶堆、小顶堆两种，在大顶堆中，父节点的值比每一个子节点的值都要大。在小顶堆中，父节点的值比每一个子节点的值都要小。

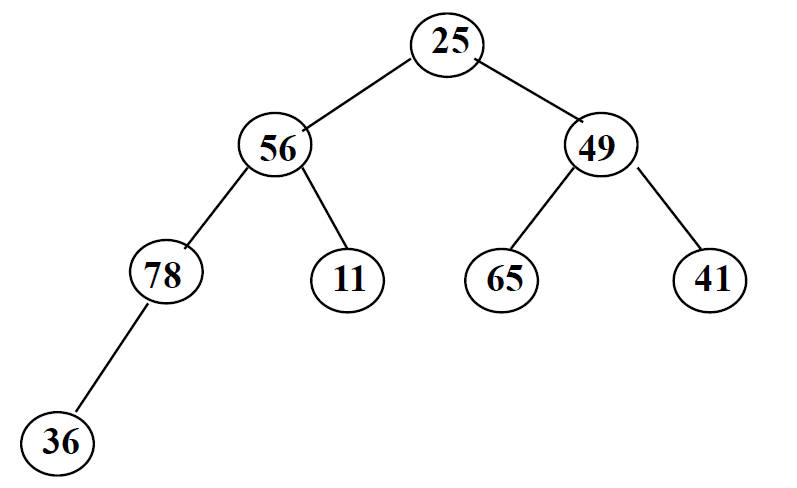
对于一个完全二叉树，我们可以按照从上到下、从左到右的顺序从1开始编号。同时我们对需要处理的数组从1进行编号

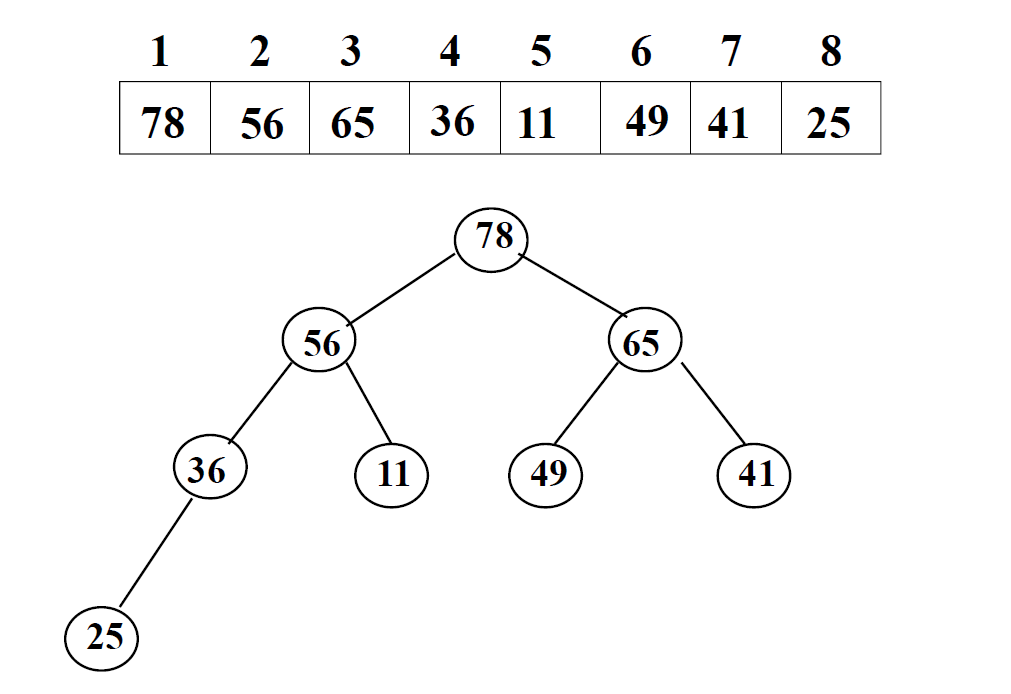
接着我们对这个二叉树进行调整（调整过程不再给出），让它满足堆的性质（以大顶堆为例，父节点的值比每一个子节点的值都要大）调整完后如下图

显然此时根节点为数组中的最大值，每次取出根节点后，对这个数组进行调整，让它接着满足堆的性质，一直取下去的话就是堆排序。

对于优先队列，我们在每次插入元素时对数组重新进行一次调整，每次取出最值后同样进行一次调整。

实际上STL里面也为我们提供了相关的实现。STL 是“Standard Template Library”的缩写，中文译为“标准模板库”。STL 是 C++ 标准库的一部分，STL 就是借助模板把常用的数据结构及其算法都实现了一遍，并且做到了数据结构和算法的分离。

STL中定义优先队列的类为priority_queue，其原型如下：

template <class T, class Container = vector<T>, class Compare = less<typename Container::value_type> > class priority_queue;

模板里面有三个参数，第一个为元素的类型，第二个为所使用的容器（vector或deque），第三个为一个比较的规则，决定是最大优先队列还是最小优先队列，默认的less为最大优先队列。

// priority_queue的主要方法
bool empty() const;
size_type size() const;
const value_type& top() const;
void push (const value_type& val);
void pop();

在使用时都要加上queue头文件
最大优先队列声明为：priority_queue<int> q
最小优先队列声明：priority_queue<int, vector<int>, greater<int> > q2

#include<queue>
#include<iostream>
using namespace std;
int main()
{
    priority_queue<int, vector<int>, greater<int> > q;
    q.push(9);
    q.push(5);
    q.push(3);
    q.push(11);
    while(!q.empty())
    {
        int val=q.top();
        cout<<val<<" ";
        q.pop();
    }
    return 0;
}

如果我们需要使用自定义比较函数，我们可以直接选用最大优先队列，然后对<进行重载

struct fruit
{
    int price;

    // 自定义比较函数的第一种方式：重载<符号
    // 注意此处一定要声明为const，否则编译时无法通过
    // const修饰的是类函数隐藏的第一个参数 this指针，这表明this指针只读，也即类成员不可修改
    // 注意该用法只能是成员函数，要是类的静态函数或者是非成员函数就不可以在函数名后面加上const
    bool operator<(const fruit& f1) const
    {
        return this->price < f1.price;
    }
}
int main(){
    priority_queue<fruit> q;
}

下面我们来看道例题

例题一 合并果子

题目

题目链接

在一个果园里，多多已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。多多决定把所有的果子合成一堆。

每一次合并，多多可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。可以看出，所有的果子经过 n-1 次合并之后， 就只剩下一堆了。多多在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以多多在合并果子时要尽可能地节省体力。假定每个果子重量都为 1 ，并且已知果子的种类 数和每种果子的数目，你的任务是设计出合并的次序方案，使多多耗费的体力最少，并输出这个最小的体力耗费值。

例如有 3 种果子，数目依次为 1 ， 2 ， 9 。可以先将 1 、 2 堆合并，新堆数目为 3 ，耗费体力为 3 。接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 12 ，耗费体力为 12 。所以多多总共耗费体力 =3+12=15 。可以证明 15 为最小的体力耗费值。

输入格式
第一行是一个整数 n (1<= n <= 10000)，表示果子的种类数。
第二行包含 n 个整数，用空格分隔，第 i 个整数 a_i(1<= a_i <= 20000) 是第 i 种果子的数目。

输出格式
一个整数，也就是最小的体力耗费值。输入数据保证这个值小于 2^31。

样例

// 样例输入
3 
1 2 9
// 样例输出
15

其中

• 对于 30% 的数据，保证有 n < 1000
• 对于 50% 的数据，保证有 n < 5000
• 对于全部的数据，保证有 n < 10000

答案

这道题显然每次取最小的两个数即可，如果直接进行排序，每次合并果子后重新再排显然会超时。我们可以采用优先队列。代码如下

#include<queue>
#include<iostream>

using namespace std;
int n, x, ans;
priority_queue<int, vector<int>, greater<int> > q;

int main() {
    cin >> n; // cin是C++编程语言中的标准输入流对象，可以理解为scanf
    while (n--)
        cin >> x, q.push(x);
    while (q.size() >= 2) {
        int a = q.top();
        q.pop();
        int b = q.top();
        q.pop();
        ans += a + b;
        q.push(a + b);
    }
    cout << ans << endl; // cin是C++编程语言中的标准输出流对象，可以理解为printf
    return 0;
}

作业一

题目链接

写一个程序来模拟操作系统的进程调度。假设该系统只有一个CPU，每一个进程的到达时间，执行时间和运行优先级都是已知的。其中运行优先级用自然数表示，数字越大，则优先级越高。

如果一个进程到达的时候CPU是空闲的，则它会一直占用CPU直到该进程结束。除非在这个过程中，有一个比它优先级高的进程要运行。在这种情况下，这个新的（优先级更高的）进程会占用CPU，而老的只有等待。

如果一个进程到达时，CPU正在处理一个比它优先级高或优先级相同的进程，则这个（新到达的）进程必须等待。

一旦CPU空闲，如果此时有进程在等待，则选择优先级最高的先运行。如果有多个优先级最高的进程，则选择到达时间最早的。

输入格式
输入包含若干行，每一行有四个自然数（均不超过10^8），分别是进程号，到达时间，执行时间和优先级。不同进程有不同的编号，不会有两个相同优先级的进程同时到达。输入数据已经按到达时间从小到大排序。输入数据保证在任何时候，等待队列中的进程不超过15000个。

输出格式
按照进程结束的时间输出每个进程的进程号和结束时间。

样例

// 输入
1 1 5 3 
2 10 5 1 
3 12 7 2 
4 20 2 3 
5 21 9 4 
6 22 2 4 
7 23 5 2 
8 24 2 4
// 输出
1 6
3 19
5 30
6 32
8 34
4 35
7 40
2 42

分析

考虑到CPU在空闲时会从等待队列中取出优先值最高的那个任务开始运行，所以很显然这就是个优先队列。

对于刚出现的每一个任务，我们直接将它放进队列，然后在下一个任务出现前不断地挨个处理程序。如果一个程序在运行到一半的时候被中断，那么保存剩余运行时间为总运行时间后将它重新压回队列。

我们使用结构体来存放每个任务的信息。

struct task {
    int number;//任务编号
    int need;//需要时间
    int get;//出现时间
    int grade;//优先级
    bool operator < (const task &b) const {
        //给优先队列提供的运算符，我们会将优先级高的，或者是优先级相同但来的更早的任务放到堆顶
        return this->grade < b.grade  (this->grade == b.grade && this->get > b.get);
    }
};

然后是优先队列

priority_queue<task> wait;

最后是主函数

int main() {
    int num, get, times, grade;
    int time = -1;
    while (scanf("%d%d%d%d", &num, &get, &times, &grade) != EOF) {
        while ((!wait.empty()) && time + wait.top().need <= get) {
            // 队列不为空，且优先级最高的进程在新加入的事件开始前就会执行完毕
            time += wait.top().need;
            printf("%d %d\n", wait.top().number, time);
            wait.pop();
        }
        if (!wait.empty()) {
            // 队列不为空，进程执行完之前有新进程加入（不一定会抢夺，只是开始时间在原进程结束前）
            // 计算当前进程所剩完成时间，重新放入队列（新进程也会在本次循环中放入队列，让优先队列自己比较去）
            task cache = wait.top();
            wait.pop();
            cache.need -= get - time;
            wait.push(cache);
        }
        wait.push({num, times, get, grade});
        time = get;
    }
    while (!wait.empty()) {
        // 将队列中剩下的时间按照优先级、时间顺序输出
        time += wait.top().need;
        printf("%d %d\n", wait.top().number, time);
        wait.pop();
    }
    return 0;
}

答案

#include<cstdio>
#include<queue>

using namespace std;

struct task {
    int number;//任务编号
    int need;//需要时间
    int get;//出现时间
    int grade;//优先级
    bool operator < (const task &b) const {
        //给优先队列提供的运算符，我们会将优先级高的，或者是优先级相同但来的更早的任务放到堆顶
        return this->grade < b.grade  (this->grade == b.grade && this->get > b.get);
    }
};

priority_queue<task> wait;

int main() {
    int num, get, times, grade;
    int time = -1;
    while (scanf("%d%d%d%d", &num, &get, &times, &grade) != EOF) {
        while ((!wait.empty()) && time + wait.top().need <= get) {
            // 队列不为空，且优先级最高的进程在新加入的事件开始前就会执行完毕
            time += wait.top().need;
            printf("%d %d\n", wait.top().number, time);
            wait.pop();
        }
        if (!wait.empty()) {
            // 队列不为空，进程执行完之前有新进程加入（不一定会抢夺，只是开始时间在原进程结束前）
            // 计算当前进程所剩完成时间，重新放入队列（新进程也会在本次循环中放入队列，让优先队列自己比较去）
            task cache = wait.top();
            wait.pop();
            cache.need -= get - time;
            wait.push(cache);
        }
        wait.push({num, times, get, grade});
        time = get;
    }
    while (!wait.empty()) {
        // 将队列中剩下的时间按照优先级、时间顺序输出
        time += wait.top().need;
        printf("%d %d\n", wait.top().number, time);
        wait.pop();
    }
    return 0;
}